2022-2023學年北京市東城區景山學校九年級(上)月考數學試卷(12月份)
發布:2024/4/20 14:35:0
一、選擇題(每題只有一個選項符合題意,每小題2分,共16分).
-
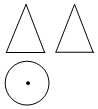 1.如圖是某幾何體的三視圖,該幾何體是( )
1.如圖是某幾何體的三視圖,該幾何體是( )A.圓錐 B.圓柱 C.三棱錐 D.長方體 組卷:53引用:2難度:0.7 -
2.在平面直角坐標系中,將拋物線y=x2向右平移2個單位長度,向上平移1個單位長度,得到拋物線( )
A.y=(x-2)2+1 B.y=(x-2)2-1 C.y=(x+2)2+1 D.y=(x+2)2-1 組卷:286引用:10難度:0.6 -
 3.在Rt△ABC中,∠C=90°,BC=4cm,AC=3cm.把△ABC繞點A順時針旋轉90°后,得到△AB1C1,如圖所示,則點B所走過的路徑長為( )
3.在Rt△ABC中,∠C=90°,BC=4cm,AC=3cm.把△ABC繞點A順時針旋轉90°后,得到△AB1C1,如圖所示,則點B所走過的路徑長為( )A.5 cm2B. πcm54C. πcm52D.5πcm 組卷:598引用:53難度:0.9 -
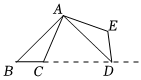 4.如圖,將△ABC繞點A逆時針旋轉100°,得到△ADE.若點D在線段BC的延長線上,則∠B的大小為( )
4.如圖,將△ABC繞點A逆時針旋轉100°,得到△ADE.若點D在線段BC的延長線上,則∠B的大小為( )A.30° B.40° C.50° D.60° 組卷:2766引用:67難度:0.9 -
5.已知⊙O的半徑為1,點P到圓心O的距離為d,若關于x的方程x2-2x+d=0有實根,則點P( )
A.在⊙O的內部 B.在⊙O的外部 C.在⊙O上 D.在⊙O上或⊙O的內部 組卷:1014引用:15難度:0.9 -
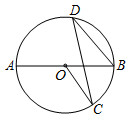 6.如圖,AB是⊙O的直徑,點C,D是圓上兩點,若∠AOC=126°,則∠CDB等于( )
6.如圖,AB是⊙O的直徑,點C,D是圓上兩點,若∠AOC=126°,則∠CDB等于( )A.27° B.37° C.54° D.64° 組卷:719引用:10難度:0.5 -
 7.如圖所示,電路連接完好,且各元件工作正常.隨機閉合開關S1,S2,S3中的兩個,能讓兩個小燈泡同時發光的概率是( )
7.如圖所示,電路連接完好,且各元件工作正常.隨機閉合開關S1,S2,S3中的兩個,能讓兩個小燈泡同時發光的概率是( )A.0 B. 12C. 13D. 14組卷:1246引用:16難度:0.5 -
8.中國科學技術館有“圓與非圓”展品,涉及了“等寬曲線”的知識.因為圓的任何一對平行切線的距離總是相等的,所以圓是“等寬曲線”.除了例以外,還有一些幾何圖形也是“等寬曲線”,如勒洛三角形(圖1),它是分別以等邊三角形的每個頂點為圓心,以邊長為半徑,在另兩個頂點間畫一段圓弧,三段圓弧圍成的曲邊三角形,圖2是等寬的勒洛三角形和圓.
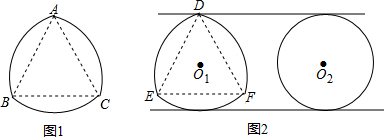
下列說法中錯誤的是( )A.勒洛三角形是軸對稱圖形 B.圖1中,點A到 上任意一點的距離都相等?BCC.圖2中,勒洛三角形上任意一點到等邊三角形DEF的中心O1的距離都相等 D.圖2中,勒洛三角形的周長與圓的周長相等 組卷:210引用:8難度:0.6
二、填空題(每小題2分,共16分).
-
9.正五邊形的每個內角為 度.
組卷:95引用:14難度:0.9
三、解答題(本題共68分,第17-19題,每題5分,第20-21題,每題6分,第22-23題,每題5分,第24題6分,25題5分,第26題6分,第27-28題,每題7分)解答應寫出文字說明、演算步驟或證明過程.
-
27.在△ABC中,AB=AC,過點C作射線CB',使∠ACB'=∠ACB(點B'與點B在直線AC的異側)點D是射線CB'上一動點(不與點C重合),點E在線段BC上,且∠DAE+∠ACD=90°.
(1)如圖1,當點E與點C重合時,AD與CB'的位置關系是 ,若BC=a,則CD的長為 ;(用含a的式子表示)
(2)如圖2,當點E與點C不重合時,連接DE.
①用等式表示∠BAC與∠DAE之間的數量關系,并證明;
②用等式表示線段BE,CD,DE之間的數量關系,并證明.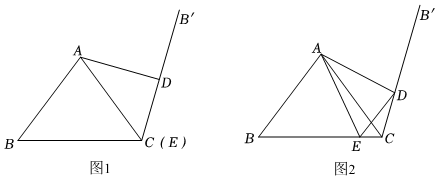 組卷:2418引用:19難度:0.4
組卷:2418引用:19難度:0.4 -
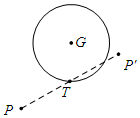 28.對于平面內點P和⊙G,給出如下定義:T是⊙G上任意一點,點P繞點T旋轉180°后得到點P',則稱點P'為點P關于⊙G的旋轉點.如圖為點P及其關于⊙G的旋轉點P'的示意圖.
28.對于平面內點P和⊙G,給出如下定義:T是⊙G上任意一點,點P繞點T旋轉180°后得到點P',則稱點P'為點P關于⊙G的旋轉點.如圖為點P及其關于⊙G的旋轉點P'的示意圖.
在平面直角坐標系xOy中,⊙O的半徑為1,點P(0,-2).
(1)在點A(-1,0),B(0,4),C(2,2)中,是點P關于⊙O的旋轉點的是 ;
(2)若在直線y=x+b上存在點P關于⊙O的旋轉點,求b的取值范圍;
(3)若點D在⊙O上,⊙D的半徑為1,點P關于⊙D的旋轉點為點P',請直接寫出點P'的橫坐標xP′的取值范圍. 組卷:546引用:3難度:0.1
組卷:546引用:3難度:0.1


