大綱版高一（上）高考題同步試卷：三 對數(shù)與對數(shù)函數(shù)（02）

一、選擇題（共16小題）

• 1．函數(shù)y=

  2

  x

  （x≥0）的反函數(shù)為（　　）

  A．y= x 2 4 （x∈R）

  B．y= x 2 4 （x≥0）

  C．y=4x2（x∈R）

  D．y=4x2（x≥0）
  組卷：933引用：44難度：0.9

  解析

• 2．設(shè)f^-1（x）為函數(shù)f（x）=

  x

  的反函數(shù)，下列結(jié)論正確的是（　　）

  A．f-1（2）=2

  B．f-1（2）=4

  C．f-1（4）=2

  D．f-1（4）=4
  組卷：565引用：34難度：0.9

  解析

• 3．已知函數(shù)f（x）=x（lnx-ax）有兩個(gè)極值點(diǎn)，則實(shí)數(shù)a的取值范圍是（　　）

  A．（-∞，0）

  B．（0， 1 2 ）

  C．（0，1）

  D．（0，+∞）
  組卷：3721引用：141難度：0.7

  解析

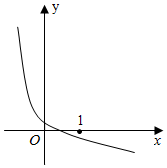• 4．已知函數(shù)y=log_a（x+c）（a,c為常數(shù)，其中a＞0，a≠1）的圖象如圖所示，則下列結(jié)論成立的是（　　）

  A．a(chǎn)＞1，c＞1	B．a(chǎn)＞1，0＜c＜1
  C．0＜a＜1，c＞1	D．0＜a＜1，0＜c＜1
  組卷：4237引用：45難度：0.9

  解析

• 5．以下四個(gè)數(shù)中的最大者是（　　）

  A．（ln2）2

  B．ln（ln2）

  C．ln 2

  D．ln2
  組卷：1002引用：43難度：0.9

  解析

• 6．已知y=log_a（2-x）是x的增函數(shù)，則a的取值范圍是（　　）

  A．（0，2）

  B．（0，1）

  C．（1，2）

  D．（2，+∞）
  組卷：688引用：37難度：0.9

  解析

• 7．函數(shù)y=e^x+1（x∈R）的反函數(shù)是（　　）

  A．y=1+lnx（x＞0）	B．y=1-lnx（x＞0）
  C．y=-1-lnx（x＞0）	D．y=-1+lnx（x＞0）
  組卷：474引用：36難度：0.9

  解析

• 8．若函數(shù)y=f（x）的圖象與函數(shù)y=ln

  x

  +

  1

  的圖象關(guān)于直線y=x對稱，則f（x）=（　　）

  A．e2x-2

  B．e2x

  C．e2x+1

  D．e2x+2
  組卷：1152引用：37難度：0.9

  解析

三、解答題（共6小題）

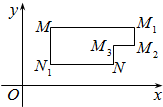• 25．在平面直角坐標(biāo)系xOy中，將從點(diǎn)M出發(fā)沿縱、橫方向到達(dá)點(diǎn)N的任一路徑稱為M到N的一條“L路徑”．如圖所示的路徑MM₁M₂M₃N與路徑MN₁N都是M到N的“L路徑”．某地有三個(gè)新建居民區(qū)，分別位于平面xOy內(nèi)三點(diǎn)A（3，20），B（-10，0），C（14，0）處．現(xiàn)計(jì)劃在x軸上方區(qū)域（包含x軸）內(nèi)的某一點(diǎn)P處修建一個(gè)文化中心．
  （I）寫出點(diǎn)P到居民區(qū)A的“L路徑”長度最小值的表達(dá)式（不要求證明）；
  （II）若以原點(diǎn)O為圓心，半徑為1的圓的內(nèi)部是保護(hù)區(qū)，“L路徑”不能進(jìn)入保護(hù)區(qū)，請確定點(diǎn)P的位置，使其到三個(gè)居民區(qū)的“L路徑”長度之和最小．
  組卷：523引用：27難度：0.1

  解析

• 26．某村莊擬修建一個(gè)無蓋的圓柱形蓄水池（不計(jì)厚度）．設(shè)該蓄水池的底面半徑為r米，高為h米，體積為V立方米．假設(shè)建造成本僅與表面積有關(guān)，側(cè)面積的建造成本為100元/平方米，底面的建造成本為160元/平方米，該蓄水池的總建造成本為12000π元（π為圓周率）．
  （Ⅰ）將V表示成r的函數(shù)V（r），并求該函數(shù)的定義域；
  （Ⅱ）討論函數(shù)V（r）的單調(diào)性，并確定r和h為何值時(shí)該蓄水池的體積最大．
  組卷：1577引用：67難度：0.5

  解析