2003年第1屆“創新杯”全國數學邀請賽試卷（初二第2試）

一、選擇題（共10小題，每小題4分，滿分40分）

• 1．計算，

  1

  ⎷

  7

  +

  4

  √

  3

  +

  1

  √

  7

  -

  4

  √

  3

  所得的值是（　　）

  A． 2 √ 3

  B．4

  C． - 2 √ 3

  D．-4
  組卷：104引用：3難度：0.9

  解析

• 2．如果x³+ax²+bx+8有兩個因式x+1和x+2，則a+b=（　　）

  A．7

  B．8

  C．15

  D．21
  組卷：593引用：6難度：0.9

  解析

• 3．△ABC周長是24，M是AB的中點，MC=MA=5，則△ABC的面積是（　　）

  A．12

  B．16

  C．24

  D．30
  組卷：863引用：5難度：0.9

  解析

• 4．某商品原價為100元，現有下列四種調價方案，其中0＜n＜m＜100，則調價后該商品價格最低的方案是（　　）

  A．先漲價m%，再降價n%

  B．先漲價n%，再降價m%

  C．行漲價 m + n 2 %，再降價 m + n 2 %

  D．先漲價 √ mn %，再降價 √ mn %
  組卷：1115引用：24難度：0.7

  解析

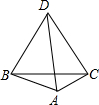• 5．在凸四邊形ABCD中，DA=DB=DC=BC，則這個四邊形中最大角的度數是（　　）

  A．120°

  B．135°

  C．150°

  D．165°
  組卷：139引用：3難度：0.9

  解析

• 6．已知a≠0，14（a²+b²+c²）=（a+2b+3c）²，那么a：b：c=（　　）

  A．2：3：6

  B．1：2：3

  C．1：3：4

  D．1：2：4
  組卷：355引用：3難度：0.9

  解析

• 7．化簡

  a

  2

  （

  1

  b

  -

  1

  c

  ）

  +

  b

  2

  （

  1

  c

  -

  1

  a

  ）

  +

  c

  2

  （

  1

  a

  -

  1

  b

  ）

  a

  （

  1

  b

  -

  1

  c

  ）

  +

  b

  （

  1

  c

  -

  1

  a

  ）

  +

  c

  （

  1

  a

  -

  1

  b

  ）

  的結果是（　　）

  A．abc

  B．a+b+c

  C． abc a + b + c

  D．-（a+b+c）
  組卷：725引用：2難度：0.5

  解析

三、解答題（共2小題，滿分20分）

• 21．已知

  a

  1

  +

  a

  +

  ab

  +

  b

  1

  +

  b

  +

  bc

  +

  c

  1

  +

  c

  +

  ca

  =

  1

  ，求證：abc=1．
  組卷：838引用：1難度：0.1

  解析

• 22．正方形ABCD中，AC=2

  √

  2

  ，則正方形的面積為

   

  ．
  組卷：19引用：1難度：0.5

  解析