2022-2023學年浙江省A9協作體高三（上）暑假返校數學試卷

一、單項選擇題：（本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的）.

• 1．已知集合A={x|2x-4≥0}，B={x||x|＜4}，則A∩B=（　　）

  A．{x|-4＜x≤2}

  B．{x|-4＜x＜4}

  C．{x|2≤x＜4}

  D．{4}
  組卷：87引用：1難度：0.7

  解析

• 2．已知i是虛數單位，復數z滿足（1+i）z=-2i,則|z|=（　　）

  A． 2

  B．1-i

  C．2

  D．1
  組卷：189引用：4難度：0.8

  解析

• 3．若圓C：x²+（y-a）²=r²（r為圓C的半徑）關于直線l：x-y+1=0對稱，則a=（　　）

  A．1

  B．-1

  C．r

  D．-r
  組卷：209引用：2難度：0.5

  解析

• 4．已知

  a

  =

  0

  .

  2

  3

  ，

  b

  =

  log

  0

  .

  4

  2

  ，

  c

  =

  π

  0

  .

  2

  ，則（　　）

  A．a＜b＜c

  B．a＜c＜b

  C．b＜c＜a

  D．b＜a＜c
  組卷：99引用：2難度：0.7

  解析

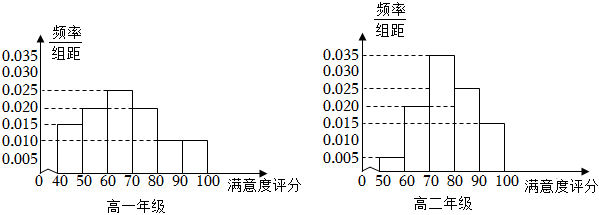• 5．某學校食堂為了解學生對食堂的滿意度，從高一、高二兩個年級分別隨機調查了100名學生，根據學生對食堂的滿意度評分，分別得到高一和高二學生滿意度評分的頻率分布直方圖．若高一和高二學生的滿意度評分中位數分別為x₁，x₂，平均數分別為y₁，y₂，則（　　）

  A．x1＞x2，y1＞y2	B．x1＞x2，y1＜y2
  C．x1＜x2，y1＜y2	D．x1＜x2，y1＞y2
  組卷：99引用：1難度：0.7

  解析

• 6．若

  α

  +

  β

  =

  π

  6

  ，且

  2

  +

  cosα

  sinα

  =

  sin

  2

  β

  1

  +

  cos

  2

  β

  ，則cosβ=（　　）

  A． - 3 4

  B． 3 4

  C． - 1 4

  D． 1 4
  組卷：203引用：1難度：0.7

  解析

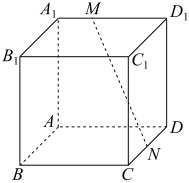• 7．在正方體ABCD-A₁B₁C₁D₁中，M是棱A₁D₁上的點且A₁M=

  1

  2

  MD₁，N是棱CD上的點，記MN與BC所成的角為α，MN與底面ABCD所成的角為β．二面角M-CD-A的平面角為γ，則（　　）

  A．α≥β≥γ

  B．α≥γ≥β

  C．γ≥α≥β

  D．γ≥β≥α
  組卷：148引用：3難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應寫出必要的文字說明、證明過程或演算步驟.

• 21．已知直線l：y=kx+1與雙曲線C：

  x

  2

  4

  -

  y

  2

  =1交于M，N兩個不同的點．
  （Ⅰ）求k的取值范圍；
  （Ⅱ）若A為雙曲線C的左頂點，點M在雙曲線C的左支上，點N在雙曲線C的右支上，且直線MA，NA分別與y軸交于P，Q兩點，當|PQ|=1時，求k的值．
  組卷：65引用：1難度：0.5

  解析

• 22．已知函數f（x）=alnx-x²（a＞0）．
  （Ⅰ）討論函數f（x）的單調性；（Ⅱ）設f（x）的導函數為f′（x），若存在x₀∈（x₁，x₂）（0＜x₁＜x₂），使得f'（x₀）=

  f

  （

  x

  2

  ）

  -

  f

  （

  x

  1

  ）

  x

  2

  -

  x

  1

  成立，求證：x₁+x₂＞2x₀．
  組卷：57引用：1難度：0.2

  解析