2022-2023學年湖北省荊州市高一(下)期中數學試卷
發布:2024/4/20 14:35:0
一、選擇題
-
1.已知
,則tanα=( )sin(α-π2)+2cos(α+5π)=2cos(α+π2)-sin(π-α)A. 13B.1 C. -13D.-1 組卷:364引用:3難度:0.7 -
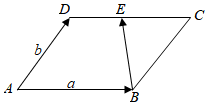 2.如圖,在平行四邊形ABCD中,E是DC的中點,若=AB,a=AD,則b=( )BE
2.如圖,在平行四邊形ABCD中,E是DC的中點,若=AB,a=AD,則b=( )BEA.- 12+abB.- 12-abC. 12+abD. 12-ab組卷:74引用:3難度:0.7 -
3.計算sin40°(
-tan10°)=( )3A.1 B.2 C. 3D.-3 組卷:309引用:5難度:0.7 -
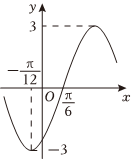 4.已知函數的部分圖像如圖所示,下列說法不正確的是( )f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)
4.已知函數的部分圖像如圖所示,下列說法不正確的是( )f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π2)A.f(x)的最小正周期為π B. f(x)=3sin(2x-π3)C.f(x)關于直線 對稱x=kπ2+5π12(k∈Z)D.將f(x)的圖像向左平移 個單位長度后得到的圖象關于原點對稱5π12組卷:61引用:5難度:0.6 -
5.已知平面向量
,a滿足|b|=|a|=2,(b+2a)?(b-a)=-2,則b與a的夾角為( )bA. π6B. π3C. 2π3D. 5π6組卷:74引用:11難度:0.9 -
6.已知
,且θ∈(3π4,π),則cosθ-sinθ=-72等于( )2cos2θ-1cos(π4+θ)A. -22B. -12C. 12D. 22組卷:541引用:5難度:0.7 -
7.在三角形△ABC中,若點P滿足
+AP=13AB,23AC,則△APQ與△ABC的面積之比為( )AQ=34AB+14ACA.1:3 B.5:12 C.3:4 D.9:16 組卷:399引用:3難度:0.7
四、解答題
-
21.已知函數f(x)=sinx?cosx-(
-1)cos2x-3cos2x-12.12
(1)求函數f(x)的單調遞增區間;
(2)將函數f(x)的圖象上每一點的橫坐標伸長原來的兩倍,縱坐標保持不變,得到函數g(x)的圖象,若方程g(x)+=0在x∈[0,π]上有兩個不相等的實數解x1,x2,求實數m的取值范圍,并求x1+x2的值.3+m2組卷:117引用:6難度:0.6 -
 22.已知平面四邊形ABCD中,AB=AD,AB⊥AD,AC=,BC=1.3
22.已知平面四邊形ABCD中,AB=AD,AB⊥AD,AC=,BC=1.3
(1)若∠ACB=,求四邊形ABCD的面積;5π6
(2)若記∠ACB=θ(0<θ<π),CD=f(θ).
①求f(θ)的解析式;
②求CD的最小值及此時角θ的值.組卷:112引用:2難度:0.6


