2022-2023學年貴州省銅仁一中高二（上）質檢數學試卷（三）（8月份）

一、單項選擇題：本大題共8個小題，每小題5分，共40分。

• 1．“-3＜m＜1”是“不等式（m-1）x²+（m-1）x-1＜0對任意的x∈R恒成立”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：697引用：21難度：0.7

  解析

• 2．已知向量

  a

  =（λ，1），

  b

  =（-1，μ），若2

  a

  +3

  b

  =（-3，8），則cos＜

  a

  ，

  a

  +

  b

  ＞=（　　）

  A． 10 10

  B． - 10 10

  C． - 3 10 10

  D． 3 10 10
  組卷：65引用：5難度：0.7

  解析

• 3．“三個臭皮匠，賽過諸葛亮”，這句口頭禪體現了集體智慧的強大．假設李某能力較強，他獨自一人解決項目M的概率為P₁=0.9；同時，有n個水平相同的人組成的團隊也在研究項目M，團隊成員各自獨立地解決項目M的概率都是0.4．如果這個n人的團隊解決項目M的概率為P₂，且P₂≥P₁，則n的取值不可能是（參考數據：lg2≈0.30，lg3≈0.48）（　　）

  A．4

  B．5

  C．6

  D．7
  組卷：164引用：3難度：0.6

  解析

• 4．已知設z=x+yi（x,y∈R），則|（x-3）+（y+3）i|=2，則|z+1|的最小值為（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：80引用：6難度：0.8

  解析

• 5．某圓臺上底面圓的半徑為1，下底面圓半徑為2，側面積為

  3

  2

  π

  ，則該圓臺的體積為（　　）

  A．3π

  B． 7 π 3

  C． 5 3 π

  D． 2 3 π
  組卷：25引用：3難度：0.8

  解析

• 6．根據氣象學上的標準，連續5天的日平均氣溫低于10℃即為入冬．將連續5天的日平均溫度的記錄數據（記錄數據都是自然數）作為一組樣本，現有4組樣本①、②、③、④，依次計算得到結果如下：
  ①平均數

  x

  ＜4；
  ②平均數

  x

  ＜4且極差小于或等于3；
  ③平均數

  x

  ＜4且標準差s≤4；
  ④眾數等于5且極差小于或等于4．
  則4組樣本中一定符合入冬指標的共有（　　）

  A．1組

  B．2組

  C．3組

  D．4組
  組卷：132引用：6難度：0.7

  解析

• 7．已知定義在R上的函數f（x）滿足：f（x）為奇函數，f（x+1）為偶函數，當0≤x≤1時，f（x）=2^x-1，則f（log₂2023）=（　　）

  A． - 999 1024

  B． - 25 2048

  C． - 1024 2023

  D． - 512 999
  組卷：196引用：5難度：0.6

  解析

四、解答題：本題共6個小題，共70分。應寫出相關演算步驟的計算公式或文字說明。

• 21．在△ABC中，內角A，B，C的對邊分別為a,b,c,已知sinA=sinB+sin（C-B）．
  （1）求角C的值；
  （2）若a＞b,且△ABC的面積

  S

  =

  3

  6

  c

  2

  ．
  （i）求證：

  c

  =

  3

  b

  ；
  （ii）已知點E在AB上，且滿足

  CA

  +

  1

  2

  CB

  =

  λ

  CE

  ，延長CE到D，使得

  CD

  =

  2

  CE

  ，連接AD，BD，求cos∠ADB．
  組卷：153引用：3難度：0.4

  解析

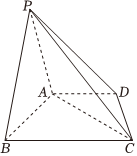• 22．如圖，在四棱錐P-ABCD中，平面PAB⊥平面ABCD，AD∥BC，

  AB

  =

  AD

  =

  CD

  =

  1

  2

  BC

  =

  2

  ．
  （1）證明：PB⊥AC；
  （2）若PA=PB，點D到平面PAC的距離為

  3

  10

  10

  ，求二面角C-PA-D的余弦值．
  組卷：9引用：2難度：0.3

  解析