2022-2023學年上海二中高一（下）期中數學試卷

一、填空題（每題3分）

• 1．一個扇形的圓心角為α弧度（0＜α＜π），扇形面積是1平方厘米，扇形半徑是1厘米，則圓心角α是

  弧度．
  組卷：13引用：1難度：0.9

  解析

• 2．函數y=tan（3x-

  π

  4

  ）的定義域為

  ．
  組卷：514引用：5難度：0.7

  解析

• 3．設

  a

  ，

  b

  是非零向量，則

  a

  =

  2

  b

  是

  a

  |

  a

  |

  =

  b

  |

  b

  |

  成立的

  條件．（用“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”填空）
  組卷：35引用：1難度：0.8

  解析

• 4．在△ABC中，BC=6，AC=8，∠A=40°，則∠B的解的個數是

  個．
  組卷：251引用：4難度：0.8

  解析

• 5．在△ABC中，AC=4，BC=3，點P是AB的中點，則

  BA

  ?

  CP

  =

  ．
  組卷：41引用：2難度：0.7

  解析

• 6．函數

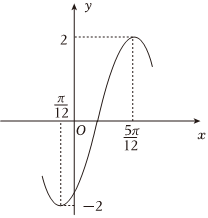  y

  =

  A

  sin

  （

  ωx

  +

  φ

  ）

  （

  A

  ＞

  0

  ，

  ω

  ＞

  0

  ，-

  π

  2

  ＜

  φ

  ＜

  π

  2

  ）

  的部分圖象如圖，若

  0

  ＜

  x

  0

  ＜

  π

  2

  ，且當x=x₀時，y=0，則x₀=

  ．
  組卷：51引用：1難度：0.5

  解析

• 7．角α是第四象限角，其終邊與單位圓的交點為

  P

  （

  4

  5

  ，-

  3

  5

  ）

  ，把角α順時針旋轉

  π

  2

  得角β，則角β終邊與單位圓的交點P′的坐標為

  ．
  組卷：142引用：3難度：0.5

  解析

三、解答題（6分+8分+8分+12分+14分）

• 20．已知△ABC中，角A，B，C的對邊分別為a,b,c,若c=5，2a=10cosB+b.
  （1）求角C；
  （2）若點D在AB邊上，且滿足AD：BD=3：2，當△ABC的面積最大時，求CD的長．
  組卷：136引用：3難度：0.6

  解析

• 21．已知函數

  f

  （

  x

  ）

  =

  si

  n

  2

  ωx

  +

  2

  3

  sinωxcosωx

  -

  co

  s

  2

  ωx

  （ω＞0）
  （1）化簡y=f（x）的表達式．
  （2）若y=f（x）的最小正周期為π，求

  y

  =

  f

  （

  x

  ）

  ，

  x

  ∈

  （

  0

  ，

  π

  2

  ）

  的單調區間
  （3）將（2）中的函數f（x）圖像上所有的點向右平移

  φ

  （

  φ

  ∈

  [

  0

  ，

  π

  2

  ]

  ）

  個單位長度，得到函數y=g（x），且y=g（x）圖像關于x=0對稱．若對于任意的實數a,函數

  y

  =

  g

  （

  λx

  ）

  ，

  x

  ∈

  [

  a

  ,

  a

  +

  π

  3

  ]

  與y=1的公共點個數不少于6個且不多于10個，求正實數λ的取值范圍．
  組卷：126引用：5難度：0.6

  解析