2022-2023學年云南省麗江市古城一中高三（下）月考數學試卷（3月份）

一、單選題

• 1．集合A={x|2≤x＜4}，B={x|x≥3}，則A∩B=（　　）

  A．[2，4）

  B．[3，+∞）

  C．[3，4）

  D．[2，3）
  組卷：25引用：6難度：0.9

  解析

• 2．

  tan

  5

  π

  4

  =（　　）

  A． - 2 2

  B． 2 2

  C．-1

  D．1
  組卷：2582引用：7難度：0.9

  解析

• 3．若函數f（x）=（1-m）lnx與

  g

  （

  x

  ）

  =

  -

  m

  2

  x

  2

  -

  （

  m

  2

  -

  m

  -

  1

  ）

  x

  -

  n

  的圖像有三個不同的交點，則實數m,n的取值范圍為（　　）

  A．m＜0，n＞0

  B．0＜m＜1，n＜0

  C．m＞0，n＞0

  D．0＜m＜1，n＞0
  組卷：23引用：1難度：0.4

  解析

• 4．設函數f（x）=lnx+ax²-

  3

  2

  x,若x=1是函數f（x）的極大值點，則函數f（x）的極小值為（　　）

  A．ln2-2

  B．ln2-1

  C．ln3-2

  D．ln3-1
  組卷：324引用：17難度：0.7

  解析

• 5．已知角α的終邊過點P（-4，3），則sinα+cosα的值是（　　）

  A． 1 5

  B．- 1 5

  C． 7 5

  D．- 7 5
  組卷：248引用：5難度：0.7

  解析

• 6．記全集U=R，集合A={x|x²-4≥0}，集合B={x|2^x≥2}，則（?_UA）∩B=（　　）

  A．[2，+∞）

  B．?

  C．[1，2）

  D．（1，2）
  組卷：59引用：2難度：0.8

  解析

• 7．在△ABC中，若AB=7，AC=5，∠ACB=120°，則BC=（　　）

  A．2 2

  B．3

  C．6

  D． 6
  組卷：1099引用：6難度：0.9

  解析

四、解答題

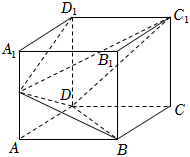• 21．如圖，在直四棱柱ABCD-A₁B₁C₁D₁中，底面ABCD為矩形，AA₁=AB=2AD=4，E在棱AA₁上．
  （1）若E為AA₁的中點，求證：平面C₁D₁E⊥平面BDE；
  （2）若二面角C₁-DE-D₁的余弦值為

  3

  3

  時，求AE的長．
  組卷：20引用：2難度：0.4

  解析

• 22．已知{a_n}為等差數列，數列{b_n}的前n項和為S_n，2a₁=b₁=2，a₂+a₈=10，_____．
  在①

  1

  2

  S

  n

  =

  b

  n

  -1，②

  b

  n

  =

  2

  λ

  a

  n

  這兩個條件中任選其中一個，補充在上面的橫線上，并完成下面問題的解答（如果選擇多個條件分別解答，按第一個解答計分）．
  （1）求數列{a_n}和{b_n}的通項公式；
  （2）求數列{a_n+b_n}的前n項和T_n．
  組卷：14引用：1難度：0.7

  解析