蘇教版（2019）必修第一冊 《第1章 集合》2020年單元測試卷

一、單項選擇題（本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．已知集合A={1，2，3}，B={2，3}，則（　　）

  A．A=B

  B．A∩B=?

  C．A?B

  D．B?A
  組卷：8792引用：33難度：0.9

  解析

• 2．下列各式中，正確的個數是（　　）
  ①{0}∈{0，1，2}；②{0，1，2}?{2，1，0}；③??{0，1，2}；
  ④?={0}；⑤{0，1}={（0，1）}；⑥0={0}．

  A．1

  B．2

  C．3

  D．4
  組卷：2116引用：33難度：0.8

  解析

• 3．集合A={0，6，8}的非空子集的個數為（　　）

  A．3

  B．6

  C．7

  D．8
  組卷：517引用：2難度：0.9

  解析

• 4．若M={x∈Z|-6≤x≤6}，N={x|x²-5x-6=0}，則M∩N=（　　）

  A．{2，3}

  B．{1，6}

  C．{-1，6}

  D．{-2，3}
  組卷：73引用：3難度：0.8

  解析

• 5．設集合M={x|x=

  k

  2

  +

  1

  4

  ，k∈Z}，集合N={x|x=

  k

  4

  +

  1

  2

  ，k∈Z}，則（　　）

  A．M=N

  B．M?N

  C．M?N

  D．M?N
  組卷：161引用：8難度：0.9

  解析

• 6．已知全集U=R，則正確表示集合M={-1，0，1}和N={x|x²+x=0}關系的韋恩（Venn）圖是（　　）

  A．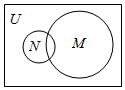

  B．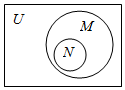

  C．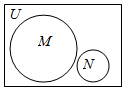

  D．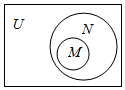
  組卷：291引用：93難度：0.9

  解析

• 7．若x∈A，則

  1

  x

  ∈A，就稱A是伙伴關系集合，集合M={-1，0，

  1

  2

  ，2，3}的所有非空子集中具有伙伴關系的集合的個數是（　　）

  A．1

  B．3

  C．7

  D．31
  組卷：497引用：7難度：0.7

  解析

四、解答題（本大題共6小題，共70分．解答時應寫出文字說明、證明過程或演算步驟）

• 21．設全集U=R，集合A={x|-5＜x＜4}，集合B={x|x＜-6或x＞1}，集合C={x|x-m＜0}，若C?（A∩B）且C?（（?_UA）∩（?_UB）），求實數m的取值范圍．
  組卷：39引用：2難度：0.7

  解析

• 22．已知集合A={x|1＜x＜3}，集合B={x|2m＜x＜1-m}．
  （1）當m=-1時，求A∪B；
  （2）若A?B，求實數m的取值范圍；
  （3）若A∩B=?，求實數m的取值范圍．
  組卷：2197引用：41難度：0.6

  解析