2023-2024學年江蘇省南京市六校聯考高三（上）月考數學試卷（8月份）

一、單項選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．若復數z滿足z（1+i）=2i,則|z|等于（　　）

  A．1

  B． 2

  C． 3

  D．2
  組卷：64引用：8難度：0.9

  解析

• 2．已知集合A={x|x²+x-2＜0}，B={x|lgx＜1}，A∩B=（　　）

  A．（-2，10）

  B．（0，1）

  C．（-2，1）

  D．（-∞，10）
  組卷：89引用：6難度：0.8

  解析

• 3．等差數列{a_n}的前n項和為S_n，且a₂=5，a₄+a₈=26，則S₇=（　　）

  A．45

  B．49

  C．56

  D．63
  組卷：171引用：2難度：0.7

  解析

• 4．從2位男生，3位女生中安排3人到三個場館做志愿者，每個場館各1人，且至少有1位男生入選，則不同安排方法有（　　）種

  A．16

  B．36

  C．54

  D．96
  組卷：179引用：1難度：0.5

  解析

• 5．“m=8”是“直線5x+12y+m=0與圓x²+y²-2x=0相切”的（　　）條件．

  A．充分不必要	B．必要不充分
  C．充要	D．既不充分也不必要
  組卷：40引用：2難度：0.6

  解析

• 6．在平面直角坐標系xOy中，雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左、右焦點分別為F₁，F₂，過F₂且垂直于x軸的直線與C交于P，Q兩點，F₁Q與y軸的交點為R，F₁Q⊥PR，則C的離心率為（　　）

  A． 2

  B． 3

  C．2

  D． 5
  組卷：1085引用：9難度：0.5

  解析

• 7．已知

  tan

  （

  π

  3

  +

  θ

  ）

  =

  3

  4

  ，則

  sin

  （

  2

  θ

  +

  π

  6

  ）

  =（　　）

  A． 24 25

  B． 7 25

  C． - 7 25

  D． - 24 25
  組卷：50引用：1難度：0.7

  解析

四、解答題：本大題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

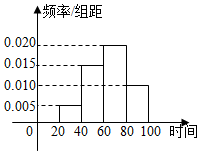• 21．2019年春節期間，我國高速公路繼續執行“節假日高速公路免費政策”．某路橋公司為掌握春節期間車輛出行的高峰情況，在某高速公路收費站點記錄了大年初三上午9：20～10：40這一時間段內通過的車輛數，統計發現這一時間段內共有600輛車通過該收費點，它們通過該收費點的時刻的頻率分布直方圖如圖所示，其中時間段9：20～9：40記作區[20，40），9：40～10：00記作[40，60），10：00～10：20記作[60，80），10：20～10：40記作[80，100），例如10點04分，記作時刻64．
  （1）估計這600輛車在9：20～10：40時間內通過該收費點的時刻的平均值（同一組中的數據用該組區間的中點值代表）；
  （2）為了對數據進行分析，現采用分層抽樣的方法從這600輛車中抽取10輛，再從這10輛車隨機抽取4輛，設抽到的4輛車中，在9：20～10：00之間通過的車輛數為X，求X的分布列與數學期望；
  （3）由大數據分析可知，車輛在每天通過該收費點的時刻T服從正態分布N（μ，σ²），其中μ可用這600輛車在9：20～10：40之間通過該收費點的時刻的平均值近似代替，σ²可用樣本的方差近似代替（同一組中的數據用該組區間的中點值代表），已知大年初五全天共有1000輛車通過該收費點，估計在9：46～10：40之間通過的車輛數（結果保留到整數）．
  若T～N（μ，σ²）則P（μ-σ＜T≤μ+σ）=0.6827，P（μ-2σ＜T≤μ+2σ）=0.9545，P（μ-3σ＜T≤μ+3σ）=0.9973．
  組卷：288引用：10難度：0.4

  解析

• 22．已知函數f（x）=e^x+x²-x,g（x）=x²+ax+b,a,b∈R．
  （1）當a=1時，求函數F（x）=f（x）-g（x）的單調區間；
  （2）若曲線y=f（x）在點（0，1）處的切線l與曲線y=g（x）切于點（1，c），求a,b,c的值；
  （3）若f（x）≥g（x）恒成立，求a+b的最大值．
  組卷：1248引用：13難度：0.1

  解析