2021-2022學(xué)年四川省攀枝花市高二（下）調(diào)研數(shù)學(xué)試卷（文科）（7月份）

一．選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．如果復(fù)數(shù)

  2

  +

  mi

  i

  （i為虛數(shù)單位，m∈R）的實部與虛部相等，那么m=（　　）

  A．-2

  B．1

  C．2022

  D．4
  組卷：14引用：2難度：0.7

  解析

• 2．觀察下列算式：2¹=2，2²=4，2³=8，2⁴=16，2⁵=32，2⁶=64，2⁷=128，2⁸=256，?，用你所發(fā)現(xiàn)的規(guī)律可得2²⁰²³的末位數(shù)字是（　　）

  A．2

  B．4

  C．6

  D．8
  組卷：4引用：1難度：0.8

  解析

• 3．下列導(dǎo)數(shù)運算正確的是（　　）

  A．（2x2+3）′=4x+3	B．（sinx）′=sinx
  C．（sinx）′=cosx	D． （ 1 x ） ′ = 1 x 2
  組卷：23引用：1難度：0.9

  解析

• 4．執(zhí)行如圖所示的程序框圖，輸出的s=（　　）
  

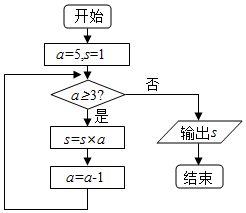
  A．5

  B．20

  C．60

  D．120
  組卷：51引用：7難度：0.9

  解析

• 5．已知8位同學(xué)某次數(shù)學(xué)測試成績的莖葉圖如圖，則下列說法正確的是（　　）

  A．眾數(shù)為7

  B．平均數(shù)為65

  C．中位數(shù)為64

  D．極差為17
  組卷：41引用：6難度：0.7

  解析

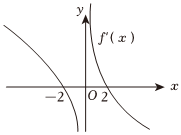• 6．函數(shù)f（x）的導(dǎo)函數(shù)為f'（x），若已知f'（x）的圖象如圖，則下列說法正確的是（　　）

  A．f（x）一定存在極小值點	B．f（x）一定有最大值
  C．f（x）在（0，+∞）單調(diào)遞減	D．不等式f（x）＞0一定有解
  組卷：15引用：2難度：0.7

  解析

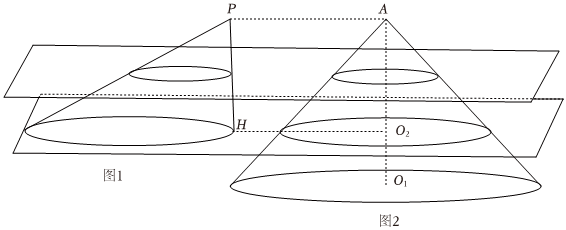• 7．我國古代數(shù)學(xué)家祖暅在求球的體積時，使用一個原理：“冪勢既同，則積不容異”．“冪”是截面積，“勢”是幾何體的高．意思是兩個等高的幾何體，如在同高處的截面積恒相等，則體積相等．如圖所示，圖1斜圓錐的高PH是圖2圓錐的高AO₁的

  2

  3

  ，若兩個幾何體被平行于圓錐底面的任意一個平面所截得的截面面積相等，且圖2圓錐的底面半徑為3，高為3，利用祖暅原理可得斜圓錐的體積為（　　）

  A． 8 π 3

  B．6π

  C． 19 π 3

  D．9π
  組卷：72引用：2難度：0.7

  解析

任選一題作答。如果多做，則按所做的第一題記分。【選修4-4：坐標(biāo)系與參數(shù)方程】（10分）

• 22．在平面直角坐標(biāo)系xOy中，直線l的傾斜角為α，其參數(shù)方程為

  x = 2 + tcosα

  y = 2 + tsinα

  （t為參數(shù)）．以坐標(biāo)原點O為極點，x軸正半軸為極軸建立極坐標(biāo)系，曲線C的極坐標(biāo)方程為ρ（ρ-4cosθ-2sinθ）=0．
  （1）求曲線C的直角坐標(biāo)方程；
  （2）若直線l過點P（2，2）與曲線C交于A，B兩點，且

  PA

  =

  -

  2

  PB

  ，求sinα．
  組卷：15引用：2難度：0.5

  解析

【選修4-5：不等式選講】（10分）

• 23．已知函數(shù)f（x）=|2x-a|+|2x+3|（a∈R）．
  （1）若a=1，解不等式f（x）≥6；
  （2）設(shè)m,n均為正數(shù)，m+2n=2，求

  m

  +

  2

  n

  的最大值．
  組卷：1引用：2難度：0.7

  解析