2023-2024學年湖北省鄂州市臨空經濟區三校聯考八年級（上）月考數學試卷（10月份）
發布：2024/9/7 6:0:11
一、選擇題（每小題3分，共30分）
-
1．如圖，在△ABC中，作BC邊上的高線，下列畫法正確的是（ ）
組卷：479引用：14難度：0.5 -
2．具備下列條件的△ABC，不是直角三角形的是（ ）
組卷：4122引用：23難度：0.5 -
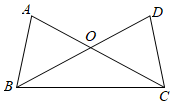3．如圖，已知AB=DC，下列條件中，不能使△ABC≌△DCB的是（ ）組卷：2559引用：39難度：0.5 -
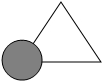4．如圖所示，亮亮書上的三角形被墨跡污染了一部分，很快他就根據所學知識畫出一個與書上完全一樣的三角形，那么這兩個三角形完全一樣的依據是（ ）組卷：2631引用：75難度：0.7 -
5．如果一個正多邊形的內角和等于720°，那么該正多邊形的一個外角等于（ ）
組卷：1466引用：29難度：0.7 -
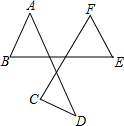6．如圖，點A、B、C、D、E、F是平面上的6個點，則∠A+∠B+∠C+∠D+∠E+∠F的度數是（ ）組卷：5806引用：36難度：0.7 -
7．在△ABC中，AC=6，中線AD=10，則AB邊的取值范圍是（ ）
組卷：1234引用：8難度：0.6 -
8．一個多邊形截去一個角后，形成的另一個多邊形的內角和是1440°，則原來多邊形的邊數是（ ）
組卷：590引用：5難度：0.6
三、解答題（17題6分；18題6分；19題8分；20題8分；21題10分；22題10分；23題12分；24題12分）
-
23．【初步探索】
（1）如圖1：在四邊形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分別是BC、CD上的點，且EF=BE+FD，探究圖中∠BAE、∠FAD、∠EAF之間的數量關系．
小王同學探究此問題的方法是：延長FD到點G，使DG=BE．連接AG，先證明△ABE≌△ADG，再證明△AEF≌△AGF，可得出結論，他的結論應是 ；
【靈活運用】
（2）如圖2，若在四邊形ABCD中，AB=AD，∠B+∠D=180°．E、F分別是BC、CD上的點，且EF=BE+FD，上述結論是否仍然成立，并說明理由；
【拓展延伸】
（3）如圖3，已知在四邊形ABCD中，∠ABC+∠ADC=180°，AB=AD，若點E在CB的延長線上，點F在CD的延長線上，如圖3所示，仍然滿足EF=BE+FD，請寫出∠EAF與∠DAB的數量關系，并給出證明過程．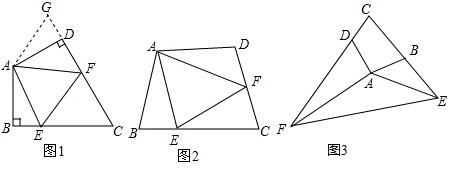
組卷：4639引用：52難度：0.1 -
24．如圖，在平面直角坐標系中，點A（-6，0），點B在y軸正半軸上，AB=BC，∠CBA=90°．
（1）如圖1，當B（0，1）時，連接AC交y軸于點D，寫出點D的坐標；
（2）如圖2，DB⊥y軸于B且BD=BO，連接CD交y軸于一點E，在B點運動的過程中，BE的長度是否會發生變化？若不變，求出BE的長度；若變化，請說明理由；
（3）如圖3，N在AC延長線上，過N（t,-6）作NQ⊥x軸于Q，探究線段BN、AQ、BO之間的數量關系，并證明你的結論．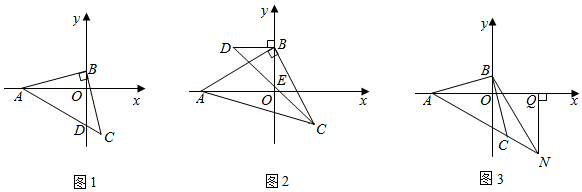
組卷：879引用：8難度：0.1