2023年云南省曲靖二中高考數學適應性試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合A={x|x＜-1或x＞1}，B={-2，-1，0，1，2}，則（?_RA）∩B=（　　）

  A．{-1，0，1}

  B．{0，1}

  C．{-1，0}

  D．{0}
  組卷：171引用：5難度：0.9

  解析

• 2．已知

  z

  =

  i

  2

  -

  i

  ，則

  z

  ?

  z

  =（　　）

  A． 5 5

  B． 1 5

  C． 5 5 i

  D． 1 5 i
  組卷：114引用：6難度：0.8

  解析

• 3．已知函數f（x）與g（x）的部分圖象如圖所示，則（　　）
  

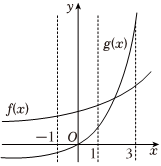
  A．g'（-1）＜0＜f'（-1）	B．f'（-1）＜0＜g'（-1）
  C．g'（3）＜f'（3）	D．f'（3）＜g'（3）
  組卷：204引用：1難度：0.8

  解析

• 4．被譽為“中國現代數學之父”的著名數學家華羅庚先生倡導的“0.618優選法”在生產和科研實踐中得到了非常廣泛的應用.0.618就是黃金分割比：

  t

  =

  5

  -

  1

  2

  的近似值，黃金分割比還可以表示成2sin18°，則

  1

  -

  2

  sin

  2

  27

  °

  t

  4

  -

  t

  2

  =（　　）

  A． 1 2

  B． 5 - 1

  C．2

  D．4
  組卷：211引用：9難度：0.7

  解析

• 5．設

  a

  ，

  b

  為單位向量，

  a

  在

  b

  方向上的投影向量為

  -

  1

  2

  b

  ，則

  |

  a

  -

  b

  |

  =（　　）

  A．1

  B． 2

  C． 3

  D．2
  組卷：85引用：3難度：0.8

  解析

• 6．若定義在R上的函數f（x）在（-∞，0]上單調遞減，且f（x）為偶函數，則不等式f（2x+3）＞f（x+1）的解集為（　　）

  A． （ - ∞ ，- 2 ） ∪ （ - 4 3 ， + ∞ ）	B． （ - ∞ ，- 4 ） ∪ （ - 2 3 ， + ∞ ）
  C． （ - 2 ，- 4 3 ）	D． （ - 4 ，- 2 3 ）
  組卷：253引用：4難度：0.7

  解析

• 7．“角谷猜想”首先流傳于美國，不久便傳到歐洲，后來一位名叫角谷靜夫的日本人又把它帶到亞洲，因而人們就順勢把它叫作“角谷猜想”．“角谷猜想”是指一個正整數，如果是奇數就乘以3再加1，如果是偶數就除以2，這樣經過若干次運算，最終回到1．對任意正整數a₀．記按照上述規則實施第n次運算的結果為a_n（n∈N），若a₅=1，且a_i（i=1，2，3，4）均不為1，則a₀=（　　）

  A．5或16

  B．5或32

  C．3或8

  D．7或32
  組卷：60引用：5難度：0.6

  解析

四、解答題：本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟．

• 21．雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左頂點為A，焦距為4，過右焦點F作垂直于實軸的直線交C于B、D兩點，且△ABD是直角三角形．
  （Ⅰ）求雙曲線C的方程；
  （Ⅱ）已知M，N是C上不同的兩點，MN中點的橫坐標為2，且MN的中垂線為直線l,是否存在半徑為1的定圓E，使得l被圓E截得的弦長為定值，若存在，求出圓E的方程；若不存在，請說明理由．
  組卷：97引用：3難度：0.5

  解析

• 22．設f（x）=xlnx-ax²+（2a-1）x,a∈R．
  （1）令g（x）=f′（x），求g（x）的單調區間；
  （2）已知f（x）在x=1處取得極大值，求實數a的取值范圍．
  組卷：1406引用：37難度：0.3

  解析