2022-2023學年山東省威海市環翠區新都中學九年級（上）期中數學試卷（五四學制）

一、選擇題（每題3分，共36分）

• 1．在函數y=

  1

  -

  x

  x

  -

  3

  中，自變量x的取值范圍是（　　）

  A．x≥0

  B．x≠3

  C．x≥0且x≠3

  D．0≤x≤3
  組卷：1423引用：4難度：0.8

  解析

• 2．如圖，在平地上種植樹木時，要求株距（相鄰兩棵樹之間的水平距離）為5m,若在坡比為i=1：2.5的山坡種樹，也要求株距為5m,那么相鄰兩棵樹間的坡面距離為（　　）
  

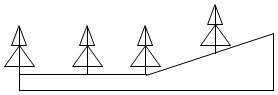
  A．2.5m

  B．5m

  C． 29 m

  D．10m
  組卷：1220引用：8難度：0.5

  解析

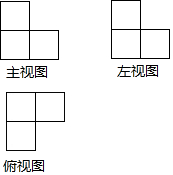• 3．一個由完全相同的小正方體組成的幾何體三視圖如圖所示，若在這個幾何體的基礎上增加幾個相同的小正方體，將其補成一個大正方體，則需要增加的小正方體的最少個數為（　　）

  A．4

  B．3

  C．6

  D．5
  組卷：377引用：4難度：0.7

  解析

• 4．二次函數y=ax²+|b|x+c,其對稱軸為直線x=-1，若

  （

  -

  14

  3

  ，

  y

  1

  ）

  ，

  （

  5

  2

  ，

  y

  2

  ）

  ，（3，y₃）是拋物線上三點，則y₁，y₂，y₃的大小關系是（　　）

  A．y1＜y2＜y3

  B．y3＜y1＜y2

  C．y3＜y2＜y1

  D．y2＜y1＜y3
  組卷：95引用：4難度：0.5

  解析

• 5．已知拋物線y=x²-4x+3與x軸相交于點A，B（點A在點B左側），頂點為M．平移該拋物線，使點M平移后的對應點M'落在x軸上，點B平移后的對應點B'落在y軸上，則平移后的拋物線解析式為（　　）

  A．y=x2+2x+1

  B．y=x2+2x-1

  C．y=x2-2x+1

  D．y=x2-2x-1
  組卷：4564引用：29難度：0.7

  解析

• 6．如圖，在半徑為

  13

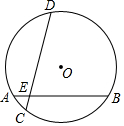  的⊙O中，弦AB與CD交于點E，∠DEB=75°，AB=6，AE=1，則CD的長是（　　）

  A．2 6

  B．2 10

  C．2 11

  D．4 3
  組卷：12154引用：31難度：0.5

  解析

• 7．已知二次函數y=x²-2px-p+3，當-1＜x＜0時，y的值恒大于1，則p的取值范圍是（　　）

  A．-1≤p≤2

  B．-3≤p≤1

  C．-1≤p≤0

  D．-3≤p≤2
  組卷：268引用：4難度：0.4

  解析

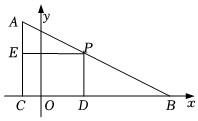• 8．如圖，在△ABC中，∠ACB=90°，BC邊在x軸上，A（-1，4），B（7，0）．點P是AB邊上一點，過點P分別作PE⊥AC于點E，PD⊥BC于點D，當四邊形CDPE的面積最大時，點P的坐標為（　　）

  A．（4， 3 2 ）

  B．（2， 5 2 ）

  C．（2，3）

  D．（3，2）
  組卷：552引用：2難度：0.3

  解析

三、解答題（共66分）

• 24．黨的二十大已經勝利閉幕，各行各業的人們用拼搏奮斗凝聚起奮進新征程、建功新時代的磅礴力量，信心滿懷向未來．某商店決定對某類商品進行降價促銷活動：已知進價為每件6元，平時以單價12元的價格售出一天可賣80件．根據調查單價每降低1元，每天可多售出40件；設商品售價x元（售價不低于進價，x為正整數），這批商品的日利潤為y元（利潤=售價-成本），請解決以下問題：
  （1）當商品的售價x為多少元時，銷售這批商品的日利潤最大，最大值為多少？
  （2）若商店每賣一件就捐m元（m＞0）給希望小學，該店發現售價為11元時可獲得最大日利潤，求m的取值范圍．
  組卷：64引用：2難度：0.5

  解析

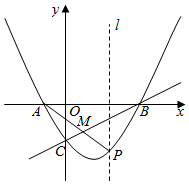• 25．已知拋物線y=ax²+bx+c與x軸交于A（-2，0）、B（6，0）兩點，與y軸交于點C（0，-3）．
  （1）求拋物線的表達式；
  （2）點P在直線BC下方的拋物線上，連接AP交BC于點M，當

  PM

  AM

  最大時，求點P的坐標及

  PM

  AM

  的最大值；
  （3）在（2）的條件下，過點P作x軸的垂線l,在l上是否存在點D，使△BCD是直角三角形，若存在，請直接寫出點D的坐標；若不存在，請說明理由．
  組卷：3530引用：10難度：0.3

  解析