2021-2022學年四川省成都七中高三（上）入學數學試卷（文科）

一、選擇題（每小題僅有一個正確選項，選對得5分，共60分）

• 1．設集合U=R，集合A={x|x²-1＞0}，B={x|0＜x≤2}，則集合（?_UA）∩B=（　　）

  A．（-1，1）

  B．[-1，1]

  C．（0，1]

  D．[-1，2]
  組卷：90引用：6難度：0.8

  解析

• 2．已知i是虛數單位，設

  z

  =

  2

  -

  3

  i

  3

  +

  2

  i

  ，則復數

  z

  +2對應的點位于復平面（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：41引用：5難度：0.8

  解析

• 3．已知向量

  BA

  =（

  1

  2

  ，

  3

  2

  ），

  BC

  =（

  3

  2

  ，

  1

  2

  ），則∠ABC=（　　）

  A．30°

  B．45°

  C．60°

  D．120°
  組卷：7562引用：33難度：0.9

  解析

• 4．小敏打開計算機時，忘記了開機密碼的前兩位，只記得第一位是M，I，N中的一個字母，第二位是1，2，3，4，5中的一個數字，則小敏輸入一次密碼能夠成功開機的概率是（　　）

  A． 8 15

  B． 1 8

  C． 1 15

  D． 1 30
  組卷：3741引用：20難度：0.9

  解析

• 5．已知數列{a_n}的前n項和為S_n，且a_n+2+a_n-2a_n+1=0（n∈N^*），若a₁₆+a₁₈+a₂₀=24，則S₃₅=（　　）

  A．140

  B．280

  C．70

  D．420
  組卷：106引用：7難度：0.7

  解析

• 6．已知命題p：存在a∈R，曲線x²+ay²=1為雙曲線；命題q：

  x

  -

  1

  x

  -

  2

  ≤0的解集是{x|1＜x＜2}．給出下列結論中正確的有（　　）
  ①命題“p且q”是真命題；
  ②命題“p且（￢q）”是真命題；
  ③命題“（￢p）或q”為真命題；
  ④命題“（￢p）或（￢q）”是真命題．

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：39引用：7難度：0.9

  解析

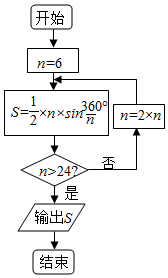• 7．公元263年左右，我國數學有劉徽發現當圓內接多邊形的邊數無限增加時，多邊形的面積可無限逼近圓的面積，并創立了割圓術，利用割圓術劉徽得到了圓周率精確到小數點后面兩位的近似值3.14，這就是著名的“徽率”．某同學利用劉徽的“割圓術”思想設計了一個計算圓周率的近似值的程序框圖如圖，則輸出S的值為
  （參考數據：sin15°=0.2588，sin7.5°=0.1305）（　　）

  A．2.598

  B．3.106

  C．3.132

  D．3.142
  組卷：17引用：8難度：0.9

  解析

三、解答題（17-21每題12分，22題10分，共70分）

• 21．已知函數f（x）=te^x-

  1

  e

  x

  -2，t∈R．
  （1）當t=-4時，求f（x）的單調區間與極值；
  （2）當t＞0時，若函數g（x）=e^xf（x）+te^x-x+1在R上有唯一零點，求t的值．
  組卷：49引用：1難度：0.5

  解析

• 22．在平面直角坐標系xOy中，已知直線l：

  x = t

  y = at

  （t為參數），以坐標原點為極點，x軸的非負半軸為極軸建立極坐標系，點A在曲線C₁：ρ²-8ρcosθ+12=0上運動，點B為線段OA的中點．
  （1）求動點B的運動軌跡C₂的參數方程；
  （2）若直線l與C₂的公共點分別為M，N，當

  |

  OM

  |

  |

  ON

  |

  =3時，求a的值．
  組卷：63引用：3難度：0.7

  解析