2022-2023學年河南省鄭州市金水區勵德雙語學校高三(上)第一次月考數學試卷(文科)
發布:2024/4/20 14:35:0
一、單選題(每題5分,共60分)
-
1.集合A={x∈N|x>6},B={x∈R|x2-3x>0},則(?NA)∩B=( )
A.{3,4,5} B.{4,5,6} C.{x|3<x≤6} D.(-∞,0)∪(3,6] 組卷:163引用:3難度:0.8 -
2.命題“?x∈[0,+∞),x3+x≥0”的否定是( )
A.?x∈(0,+∞),x3+x<0 B.?x∈(-∞,0),x3+x≥0 C.?x0∈[0,+∞),x03+x0<0 D.?x0∈[0,+∞),x03+x0≥0 組卷:8引用:3難度:0.9 -
3.函數y=(3x-3-x)cosx在區間[-
,π2]的圖像大致為( )π2A. 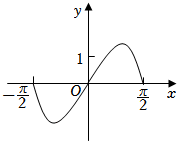
B. 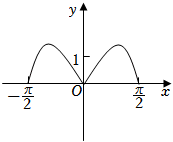
C. 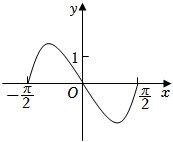
D. 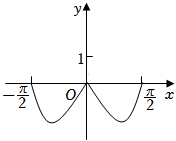 組卷:2586引用:15難度:0.6
組卷:2586引用:15難度:0.6 -
4.已知函數f(x)=
x3+ax+4,則“a>0”是“f(x)在R上單調遞增”的( )12A.充分不必要條件 B.必要不充分條件 C.充要條件 D.既不充分也不必要條件 組卷:247引用:18難度:0.9 -
5.已知函數f(x)的定義域為[-1,2],則函數
的定義域為( )g(x)=f(2x)+1-2xA.[0,1] B.[-1,0] C. [-12,1]D. [-12,0]組卷:1314引用:6難度:0.8 -
6.函數
在點(0,f(0))處的切線方程為( )f(x)=2xx+1+exA.y=3x+1 B.y=2x+1 C. y=54x+1D.y=x+1 組卷:181引用:6難度:0.7 -
7.已知函數f(x)是定義在R上的奇函數,當x<0時,f(x)=ex(x+1),則下列結論中錯誤的是( )
A.當x>0時,f(x)=-e-x(x-1) B.函數f(x)有3個零點 C.f(x)<0的解集為(-∞,-1)∪(0,1) D.?x1,x2∈R,都有|f(x1)-f(x2)|<2 組卷:317引用:4難度:0.5
三、解答題(共70分)
-
21.已知函數f(x)=x3+ax.
(1)若函數g(x)=f(x)+bx2+b2在x=1處的極值為10,求實數a,b的值;
(2)若函數h(x)=f(x)+ax2+1在區間(-2,-1)內存在單調遞減區間,求實數a的取值范圍.組卷:81引用:2難度:0.5 -
22.已知函數
.f(x)=lnx-ax+1-ax-1(a∈R)
(1)當時,討論f(x)的單調性;a≤12
(2)設g(x)=x2-2bx+4.當時,若對任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求實數b的取值范圍.a=14組卷:610引用:6難度:0.1


