2022-2023學年河北省部分學校高二（上）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．直線3x+4y-5=0的斜率為k,則k的值為（　　）

  A． 3 4

  B． 4 3

  C．- 4 3

  D．- 3 4
  組卷：28引用：2難度：0.9

  解析

• 2．橢圓

  x

  2

  4

  +

  y

  2

  8

  =

  1

  上的一點到兩個焦點的距離之和為（　　）

  A．2

  B．4

  C． 4 3

  D． 4 2
  組卷：1078引用：4難度：0.8

  解析

• 3．傾斜角為135°的直線經過點（a+1，5）和（2a-2，3a），則a=（　　）

  A．1

  B．-1

  C．2

  D．-2
  組卷：73引用：3難度：0.8

  解析

• 4．圓x²+y²-4x=0與圓（x-3）²+（y+3）²=9的公切線共有（　　）

  A．1條

  B．2條

  C．3條

  D．4條
  組卷：119引用：6難度：0.8

  解析

• 5．雙曲線

  C

  ：

  x

  2

  16

  -

  y

  2

  12

  =

  1

  上的點P到左焦點的距離為9，則P到右焦點的距離為（　　）

  A．5

  B．1

  C．1或17

  D．17
  組卷：268引用：7難度：0.7

  解析

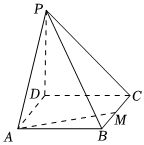• 6．如圖，四棱錐P-ABCD的底面是邊長為4的正方形，PD=8，且PA=PC=4

  5

  ，M為BC的中點，則異面直線PB與AM所成角的余弦值為（　　）

  A． 30 30

  B． 6 6

  C． 5 5

  D． 10 10
  組卷：81引用：6難度：0.6

  解析

• 7．方程

  y

  +

  1

  =

  -

  x

  2

  +

  4

  x

  表示的曲線為（　　）

  A．圓（x-2）2+（y+1）2=4

  B．圓（x-2）2+（y+1）2=4的上半部分

  C．圓（x+2）2+（y-1）2=4

  D．圓（x-2）2+（y+1）2=4的右半部分
  組卷：137引用：8難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的離心率為

  1

  2

  ，左、右焦點分別為F₁，F₂，過F₁且垂直于x軸的直線被橢圓C所截得的弦長為6．
  （1）求橢圓C的方程；
  （2）P為第一象限內橢圓C上一點，直線PF₁，PF₂與直線x=8分別交于A，B兩點，記△PAB和△PF₁F₂的面積分別為S₁，S₂，若

  S

  1

  S

  2

  =5，求P的坐標．
  組卷：36引用：5難度：0.5

  解析

• 22．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左、右焦點分別為F₁（-c,0），F₂（c,0），且與橢圓

  x

  2

  25

  +

  y

  2

  16

  =1有相同的焦點，點F₁到直線bx+ay=0的距離為2

  2

  ．
  （1）求C的標準方程；
  （2）直線

  l

  ：

  y

  =

  k

  （

  x

  -

  c

  ）

  （

  |

  k

  |

  ＜

  b

  a

  ）

  與C交于A，B兩點，點P是∠AF₁B的平分線上一動點，且

  F

  1

  P

  =

  λ

  （

  F

  1

  A

  +

  F

  1

  B

  ）

  ，證明：|AF₂|?|BF₂|=|AB|²．
  組卷：41引用：2難度：0.4

  解析