2023-2024學年山東省青島市萊西市高一（上）段考數學試卷（一）

一、單項選擇題：本大題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合M={y|y=2^x，x≤1}，

  N

  =

  {

  x

  |

  y

  =

  x

  -

  x

  2

  }

  ，則M∪N等于（　　）

  A．?

  B．{2}

  C．[0，2]

  D．（-∞，2]
  組卷：81引用：7難度：0.9

  解析

• 2．已知函數f（x）是定義在R上的函數，命題p：“函數f（x）的最小值為3”，則^?p是（　　）

  A．對任意x∈R，都有f（x）＜3

  B．存在x∈R，使得f（x）＜3

  C．對任意x∈R，都有f（x）≠3

  D．“‘存在x∈R，使得f（x）＜3’或‘對任意x∈R，都有f（x）≠3’”
  組卷：14引用：1難度：0.7

  解析

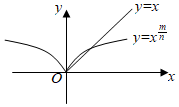• 3．如圖所示是函數y=

  x

  m

  n

  （m、n∈N^*且互質）的圖象，則（　　）

  A．m、n是奇數且 m n ＜1

  B．m是偶數，n是奇數，且 m n ＞1

  C．m是偶數，n是奇數，且 m n ＜1

  D．m、n是偶數，且 m n ＞1
  組卷：1122引用：12難度：0.7

  解析

• 4．若函數y=x²+（2a-1）x+1在區間（2，+∞）上是增函數，則實數a的取值范圍是（　　）

  A．[- 3 2 ，+∞）

  B．（-∞，- 3 2 ]

  C．[ 3 2 ，+∞）

  D．（-∞， 3 2 ]
  組卷：156引用：9難度：0.7

  解析

• 5．函數

  f

  （

  x

  ）

  =

  2

  x

  2

  3

  x

  +

  3

  -

  x

  的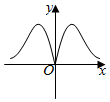圖象大致是（　　）

  A．

  B．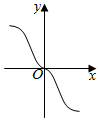

  C．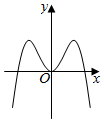

  D．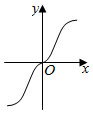
  組卷：44引用：2難度：0.7

  解析

• 6．已知函數y=f（3^x）的定義域為[1，2]，則函數

  y

  =

  f

  （

  x

  +

  1

  ）

  x

  -

  2

  的定義域為（　　）

  A．[-1，1）

  B．[0，1]

  C．（2，8]

  D．[0，2）∪（2，3]
  組卷：31引用：1難度：0.8

  解析

• 7．某食品保鮮時間y（單位：小時）與儲藏溫度x（單位：℃） 滿足函數關系y=e^kx+b （e=2.718…為自然對數的底數，k,b為常數）．若該食品在0℃的保鮮時間是192小時，在22℃的保鮮時間是48小時，則該食品在33℃的保鮮時間是（　　）

  A．16小時

  B．20小時

  C．24小時

  D．28小時
  組卷：343引用：8難度：0.7

  解析

四、解答題：共70分，解答應寫出文字說明、證明過程或演算步驟．

• 21．某群體的人均通勤時間，是指單日內該群體中成員從居住地到工作地的平均用時．某地上班族S中的成員僅以自駕或公交方式通勤．分析顯示：當S中x%（0＜x＜100）的成員自駕時，自駕群體的人均通勤時間為
  f（x）=

  30 ， 0 ＜ x ≤ 30

  2 x + 1800 x - 90 ， 30 ＜ x ＜ 100

  （單位：分鐘），而公交群體的人均通勤時間不受x影響，恒為40分鐘，試根據上述分析結果回答下列問題：
  （1）當x在什么范圍內時，公交群體的人均通勤時間少于自駕群體的人均通勤時間？
  （2）求該地上班族S的人均通勤時間g（x）的表達式；討論g（x）的單調性，并說明其實際意義．
  組卷：1638引用：26難度：0.5

  解析

• 22．設函數f（x）的定義域是（0，+∞），且對任意的正實數x、y都有f（xy）=f（x）+f（y）恒成立，已知

  f

  （

  1

  16

  ）

  =

  4

  ，且0＜x＜1時，f（x）＞0．
  （1）求f（1）與

  f

  （

  1

  2

  ）

  的值；
  （2）求證：函數f（x）在（0，+∞）上單調遞減；
  （3）解不等式

  f

  （

  x

  ）

  +

  1

  ＜

  1

  2

  f

  （

  3

  2

  x

  -

  2

  ）

  ．
  組卷：37引用：1難度：0.5

  解析