2022-2023學年江蘇省連云港市海州區新海初級中學九年級（上）第二次月考數學試卷

一、選擇題（本大題共8小題，每小題3分，共24分）

• 1．將一元二次方程3x²+4x=7化成一般式后，一次項系數和常數項分別為（　　）

  A．4，7

  B．-4，7

  C．4，-7

  D．-4，-7
  組卷：69引用：3難度：0.9

  解析

• 2．拋物線y=-（x+1）²+3的頂點坐標是（　　）

  A．（1，3）

  B．（-1，3）

  C．（-1，-3）

  D．（1，-3）
  組卷：618引用：4難度：0.6

  解析

• 3．為了調查某校同學的體質健康狀況，隨機抽查了若干名同學的每天鍛煉時間如表：
  

  每天鍛煉時間（分鐘）	20	40	60	90
  學生數	2	3	4	1

  則關于這些同學的每天鍛煉時間，下列說法錯誤的是（　　）

  A．眾數是60	B．平均數是21
  C．抽查了10個同學	D．中位數是50
  組卷：239引用：11難度：0.7

  解析

• 4．分別寫有數字0，-1，-2，1，3的五張卡片，除數字不同外其他均相同，從中任抽一張，那么抽到正數的概率是（　　）

  A． 1 5

  B． 2 5

  C． 3 5

  D． 4 5
  組卷：105引用：3難度：0.7

  解析

• 5．筒車是我國古代發明的一種水利灌溉工具，明朝科學家徐光啟在《農政全書》中用圖畫描繪了筒車的工作原理，如圖1．筒車盛水桶的運行軌道是以軸心O為圓心的圓，如圖2．已知圓心O在水面上方，且⊙O被水面截得的弦AB長為6米，⊙O半徑長為4米．若點C為運行軌道的最低點，則點C到弦AB所在直線的距離是（　　）
  

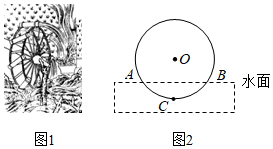
  A．1米

  B．（4- 7 ）米

  C．2米

  D．（4+ 7 ）米
  組卷：3213引用：41難度：0.7

  解析

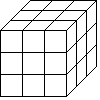• 6．如圖，將一個棱長為3的正方體表面涂上顏色，再把它分割成棱長為1的小正方體，將它們全部放入一個不透明盒子中搖勻，隨機取出一個小正方體，只有一個面被涂色的概率為（　　）

  A． 4 27

  B． 2 9

  C． 8 27

  D． 20 27
  組卷：679引用：13難度：0.9

  解析

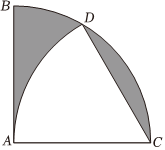• 7．如圖，在扇形ABC中，∠BAC=90°，AB=6，若以點C為圓心，CA為半徑畫弧，與

  ?

  BC

  交于點D，則圖中陰影部分的面積和是（　　）

  A．π

  B．2π

  C．3π

  D．4π
  組卷：31引用：2難度：0.6

  解析

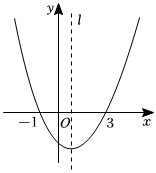• 8．如圖為二次函數y=ax²+bx+c的圖象，下列說法：①ac＜0；②2a+b=0；③a+b+c＞0；④當x＞0.5時，y隨x的增大而增大；⑤3a+c=0；⑥對于任意實數m,均有am²+bm≥a+b.正確的說法有（　　）

  A．①④⑤⑥

  B．①②③⑤

  C．①③④⑥

  D．①②⑤⑥
  組卷：58引用：3難度：0.5

  解析

三、解答題（本大題共10小題，共102分）

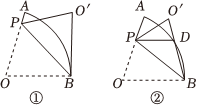• 25．在扇形AOB中，半徑OA=6，點P在OA上，連接PB，將△OBP沿著PB折疊得到△O'BP．
  （1）如圖①，若∠O=75°，且BO'與

  ?

  AB

  所在的圓相切于點B．
  ①∠APO'=

  °；
  ②求OP的長；
  （2）如圖②，BO'與

  ?

  AB

  相交于點D，若點D為

  ?

  AB

  的中點，且PD∥OB，求

  ?

  AB

  的長．
  組卷：53引用：2難度：0.3

  解析

• 26．如圖1，在平面直角坐標系xOy中，拋物線

  F

  1

  ：

  y

  =

  x

  2

  +

  bx

  +

  c

  經過點A（-3，0）和點B（1，0）．
  
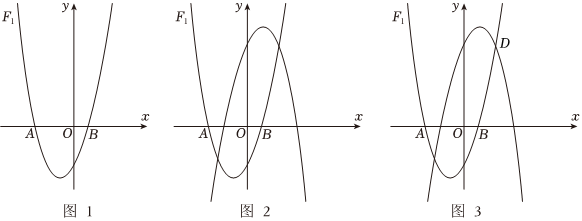
  （1）拋物線F₁的表達式為

  ，它的頂點坐標為

  ；
  （2）如圖2，作拋物線F₂，使它與拋物線F₁關于原點O成中心對稱，拋物線F₂的表達式為

  ；
  （3）如圖3，將（2）中拋物線F₂向上平移2個單位，得到拋物線F₃，拋物線F₁與拋物線F₃相交于C，D兩點（點C在點D的左側）．
  ①求點C和點D的坐標；
  ②若點M，N分別為拋物線F₁和拋物線F₃上C，D之間的動點（點M，N與點C，D不重合），試求四邊形CMDN面積的最大值．
  組卷：52引用：2難度：0.3

  解析