2022-2023學年陜西省榆林市橫山中學高二（下）期中數學試卷（文科）

一、選擇題：本大題共12小題．每小題5分，共60分，在每個小題給出的四個選項中，只有一項是符合要求的.

• 1．命題：?x∈R，x+lnx＞0的否定是（　　）

  A．?x?R，x+lnx＞0	B．?x?R，x+lnx≤0
  C．?x∈R，x+lnx＞0	D．?x∈R，x+lnx≤0
  組卷：152引用：5難度：0.8

  解析

• 2．已知集合A={x|x²＜8}，B={x|1-x≤0}，則A∩B=（　　）

  A．[-1，2）

  B． [ 1 ， 2 2 ）

  C．[1，2）

  D．[0，3）
  組卷：171引用：6難度：0.8

  解析

• 3．已知復數z滿足i（z+1）=-1+2i（其中i為虛數單位），則

  z

  =（　　）

  A．1-i

  B．1+i

  C．-3-i

  D．-3+i
  組卷：64引用：3難度：0.8

  解析

• 4．點P的直角坐標為

  （

  -

  2

  ，

  2

  ）

  ，那么它的極坐標可表示為（　　）

  A． （ 2 ， 3 π 4 ）

  B． （ 2 ， 5 π 4 ）

  C． （ 1 ， 5 π 4 ）

  D． （ 1 ， 3 π 4 ）
  組卷：24引用：1難度：0.9

  解析

• 5．已知均為實數a,b,c,d,且a＞b＞0＞c＞d,則下列不等式成立的是（　　）

  A．a2＞c2	B．ln（ab）＞ln（cd）
  C． c a ＞ d b	D．2-c＞2-d
  組卷：39引用：1難度：0.7

  解析

• 6．已知復數z滿足

  2

  （

  z

  -

  z

  ）

  +

  z

  ?

  z

  =

  2

  +

  4

  i

  ，z在復平面內對應的點在第二象限，則z=（　　）

  A．-1-i

  B．1+i

  C．-1+i

  D．-2+i
  組卷：117引用：5難度：0.8

  解析

• 7．已知直線的參數方程為

  x = 3 - tsin 20 °

  y = 2 + tcos 70 °

  ，則該直線的傾斜角為（　　）

  A．20°

  B．45°

  C．110°

  D．135°
  組卷：78引用：3難度：0.7

  解析

三、解答題（本大題共6小題，共70分解答應寫出文字說明、證明過程或演算步驟）

• 21．在平面直角坐標系xOy中，直線l₁的參數方程為

  x = t

  y = kt

  （t為參數），直線l₂的參數方程為

  x = - km + 2

  y = m

  （m為參數），設直線l₁與l₂的交點為P，當k變化時點P的軌跡為曲線C₁．
  （Ⅰ）求曲線C₁的軌跡方程；
  （Ⅱ）以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，直線C₂的極坐標方程為ρsin（θ+

  π

  4

  ）=3

  2

  ，點Q為曲線C₁上的動點，求點Q到直線C₂距離的最大值．
  組卷：16引用：1難度：0.4

  解析

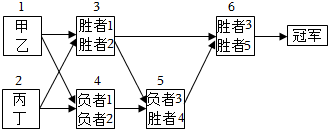• 22．甲、乙、丙、丁4名棋手進行象棋比賽，賽程如下面的框圖所示，其中編號為i的方框表示第i場比賽，方框中是進行該場比賽的兩名棋手，第i場比賽的勝者稱為“勝者i”，負者稱為“負者i”，第6場為決賽，獲勝的人是冠軍．已知甲每場比賽獲勝的概率均為

  3

  4

  ，而乙、丙、丁相互之間勝負的可能性相同．
  （1）求乙獲連負兩場的概率；
  （2）求甲獲得冠軍的概率；
  （3）求乙進入決賽，且乙與其決賽對手是第二次相遇的概率．
  組卷：386引用：3難度：0.4

  解析