當前位置：試卷中心 > 試卷詳情

2023-2024學年黑龍江省大慶鐵人中學高二（上）期中數學試卷

發布：2024/10/23 15:0:2

一、單選題（每小題只有一個選項正確，共8小題，每小題5分，共40分。）

1．經過點（-1，2）并且與直線2x+y-1=0垂直的直線方程是（　　）
A．x-2y+5=0 B．x-2y+3=0 C．x+2y-3=0 D．x+2y+5=0
組卷：103引用：5難度：0.5
解析
2．曲線
x
2
25
+
y
2
9
=1與曲線
x
2
25
-
k
+
y
2
9
-
k
=1（k＜9）的（　　）
A．長軸長相等 B．短軸長相等 C．離心率相等 D．焦距相等
組卷：2988引用：98難度：0.9
解析
3．已知向量
a
=（1，1，0），
b
=（-1，0，2），且k
a
+
b
與2
a
+
b
互相垂直，則k的值是（　　）
A．-1 B．
4
3
C．
5
3
D．
7
5
組卷：163引用：4難度：0.8
解析
4．已知圓M經過點A（-1，-4），B（6，3），且圓心在直線x-y-4=0上，則圓C的標準方程為（　　）
A．（x-3）²+（y+1）²=25 B．（x-3）²+（y-1）²=25
C．（x-3）²+（y+1）²=5 D．（x+3）²+（y+1）²=25
組卷：241引用：3難度：0.5
解析
5．設B是橢圓C：
x
2
5
+y²=1的上頂點，點P在C上，則|PB|的最大值為（　　）
A．
5
2
B．
6
C．
5
D．2
組卷：6050引用：14難度：0.5
解析
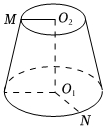6．如圖，圓臺的高為4，上、下底面半徑分別為3、5，M、N分別在上、下底面圓周上，且＜
O
2
M
，
O
1
N
＞=120°，則|
MN
|等于（　　）
A．
65
B．5
2
C．
35
D．5
組卷：204引用：10難度：0.9
解析
7．已知F₁，F₂是雙曲線C的兩個焦點，P為C上一點，且∠F₁PF₂=60°，|PF₁|=3|PF₂|，則C的離心率為（　　）
A．
7
B．
13
C．
7
2
D．
13
2
組卷：3255引用：41難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（共6小題，共70分。）

21．如圖，AE⊥平面ABCD，CF∥AE，AD∥BC，AD⊥AB，AB=AD=2，AE=BC=4．?
（1）求直線CE與平面BDE所成角的正弦值；
（2）若二面角E-BD-F的余弦值為
1
3
，求線段CF的長．
組卷：27引用：2難度：0.4
解析
22．如圖：小明同學先把一根直尺固定在畫板上面，把一塊三角板的一條直角邊緊靠在直尺邊沿，再取一根細繩，它的長度與另一直角邊相等，讓細繩的一端固定在三角板的頂點A處，另一端固定在畫板上點F處，用鉛筆尖扣緊繩子（使兩段細繩繃直），靠住三角板，然后將三角板沿著直尺上下滑動，這時筆尖在平面上畫出了圓錐曲線C的一部分圖象．已知細繩長度為3，經測量，當筆尖運動到點P處，此時，∠FAP=30°，∠AFP=90°．設直尺邊沿所在直線為a,以過F垂直于直尺的直線為x軸，以過F垂直于a的垂線段的中垂線為y軸，建立平面直角坐標系．
（1）求曲線C的方程；
（2）斜率為k的直線過點D（0，-3），且與曲線C交于不同的兩點M，N，已知k的取值范圍為（0，2），探究：是否存在λ，使得
DM
=
λ
DN
，若存在，求出λ的范圍，若不存在，說明理由．
組卷：129引用：9難度：0.5
解析