2012-2013學(xué)年山東省高二（下）數(shù)學(xué)暑假作業(yè)（六）（文科）

一、選擇題

• 1．集合A={0，2，a}，B={1，a²}，若A∪B={0，1，2，4，16}，則a的值為（　　）

  A．0

  B．1

  C．2

  D．4
  組卷：1571引用：127難度：0.9

  解析

• 2．i是虛數(shù)單位，若

  1

  +

  7

  i

  2

  -

  i

  =a+bi（a,b∈R），則乘積ab的值是（　　）

  A．-15

  B．-3

  C．3

  D．15
  組卷：461引用：41難度：0.9

  解析

• 3．命題“存在x₀∈R，

  2

  x

  0

  ≤0”的否定是（　　）

  A．不存在x0∈R， 2 x 0 ＞0	B．存在x0∈R， 2 x 0 ≥0
  C．對(duì)任意的x∈R，2x≤0	D．對(duì)任意的x∈R，2x＞0
  組卷：264引用：160難度：0.9

  解析

• 4．已知a∈R，則“a＜2”是“|x-2|+|x|＞a恒成立”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：27引用：16難度：0.9

  解析

• 5．已知函數(shù)f（x）滿足：x≥4，則f（x）=

  （

  1

  2

  ）

  x

  ；當(dāng)x＜4時(shí)f（x）=f（x+1），則f（2+log₂3）=（　　）

  A． 1 24

  B． 1 12

  C． 1 8

  D． 3 8
  組卷：1355引用：42難度：0.9

  解析

• 6．已知函數(shù)f（x+1）是偶函數(shù)，當(dāng)1＜x₁＜x₂時(shí)，

  f

  （

  x

  2

  ）

  -

  f

  （

  x

  1

  ）

  x

  2

  -

  x

  1

  ＞

  0

  恒成立，設(shè)a=f（-

  1

  2

  ），b=f（2），c=f（3），則a,b,c的大小關(guān)系為（　　）

  A．a(chǎn)＜b＜c

  B．c＜b＜a

  C．b＜c＜a

  D．b＜a＜c
  組卷：15引用：2難度：0.7

  解析

三、解答題

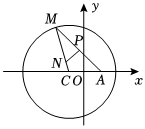• 19．（理）如圖所示，已知圓C：（x+1）²+y²=8，定點(diǎn)A（1，0），M為圓上一動(dòng)點(diǎn)，點(diǎn)P在AM上，點(diǎn)N在CM上，且滿足

  AM

  =

  2

  AP

  ，

  NP

  ?

  AM

  =0，|CN|+|NM|=2

  2

  ，點(diǎn)N的軌跡為曲線E．
  （1）求曲線E的方程；
  （2）過(guò)點(diǎn)S（0，

  1

  3

  ）且斜率為k的動(dòng)直線l交曲線E于A、B兩點(diǎn)，在y軸上是否存在定點(diǎn)G，滿足

  GP

  =

  GA

  +

  GB

  使四邊形NAPB為矩形？若存在，求出G的坐標(biāo)和四邊形NAPB面積的最大值；若不存在，說(shuō)明理由．
  組卷：62引用：4難度：0.3

  解析

• 20．設(shè)函數(shù)f（x）=（2-a）lnx+

  1

  x

  +2ax.
  （Ⅰ）當(dāng)a=0時(shí)，求f（x）的極值；
  （Ⅱ）當(dāng)a≠0時(shí)，求f（x）的單調(diào)區(qū)間；
  （Ⅲ）當(dāng)a=2時(shí)，對(duì)任意的正整數(shù)n,在區(qū)間[

  1

  2

  ，6+n+

  1

  n

  ]上總有m+4個(gè)數(shù)使得f（a₁）+f（a₂）+f（a₃）+…+f（a_m）＜f（a_m+1）+f（a_m+2）+f（a_m+3）+f（a_m+4）成立，試問(wèn)：正整數(shù)m是否存在最大值？若存在，求出這個(gè)最大值；若不存在，說(shuō)明理由．
  組卷：58引用：5難度：0.1

  解析