2022-2023學(xué)年山東省聊城一中高二（下）期中數(shù)學(xué)試卷

一、單選題：本大題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一個(gè)選項(xiàng)符合題目要求．

• 1．已知函數(shù)y=f（x）在x=x₀處的導(dǎo)數(shù)f′（x₀）=-1，則

  lim

  Δ

  x

  →

  0

  f

  （

  x

  0

  +

  2

  Δ

  x

  ）

  -

  f

  （

  x

  0

  ）

  Δ

  x

  =（　　）

  A．-1

  B．1

  C． 1 2

  D．-2
  組卷：23引用：3難度：0.8

  解析

• 2．學(xué)校食堂的一個(gè)窗口共賣5種菜，甲、乙、丙3名同學(xué)每人從中選一種，假設(shè)每種菜足量，則不同的選法共有（　　）

  A．35種

  B．53種

  C． A 3 5 種

  D． C 3 5 種
  組卷：99引用：3難度：0.7

  解析

• 3．設(shè)某芯片制造廠有甲、乙兩條生產(chǎn)線均生產(chǎn)5nm規(guī)格的芯片，現(xiàn)有20塊該規(guī)格的芯片，其中甲、乙生產(chǎn)的芯片分別為12塊，8塊，且乙生產(chǎn)該芯片的次品率為

  1

  20

  ，現(xiàn)從這20塊芯片中任取一塊芯片，若取得芯片的次品率為0.08，則甲廠生產(chǎn)該芯片的次品率為（　　）

  A． 1 5

  B． 1 10

  C． 1 15

  D． 1 20
  組卷：64引用：7難度：0.7

  解析

• 4．若

  （

  x

  -

  2

  x

  2

  ）

  n

  的展開式中只有第6項(xiàng)的二項(xiàng)式系數(shù)最大，則該二項(xiàng)式的展開式中常數(shù)項(xiàng)為（　　）

  A．90

  B．-90

  C．180

  D．-180
  組卷：423引用：8難度：0.8

  解析

• 5．函數(shù)f（x）=

  e

  x

  -

  e

  -

  x

  x

  2

  的圖象大致為（　　）

  A．

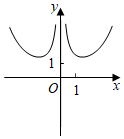
  B．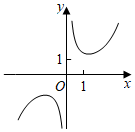

  C．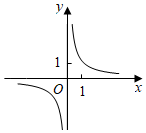

  D．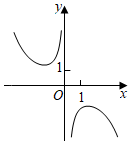
  組卷：1957引用：128難度：0.9

  解析

• 6．中國(guó)古代中的“禮、樂(lè)、射、御、書、數(shù)”合稱“六藝”．“禮”，主要指德育；“樂(lè)”，主要指美育；“射”和“御”，就是體育和勞動(dòng)；“書”，指各種歷史文化知識(shí)；“數(shù)”，數(shù)學(xué)．某校國(guó)學(xué)社團(tuán)開展“六藝”課程講座活動(dòng)，每藝安排一節(jié)，連排六節(jié)，一天課程講座排課有如下要求：“數(shù)”必須排在前三節(jié)，且“射”和“御”兩門課程相鄰排課，則“六藝”課程講座不同排課順序共有（　　）

  A．120種

  B．156種

  C．188種

  D．240種
  組卷：683引用：10難度：0.5

  解析

• 7．在（1+x）+（1+x）²+（1+x）³+…+（1+x）⁹的展開式中，x³的系數(shù)為（　　）

  A．120

  B．210

  C．720

  D．5040
  組卷：138引用：8難度：0.7

  解析

四、解答題：本題共7小題，共70分．解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟．

• 22．已知函數(shù)f（x）=lnx+

  a

  x

  ，a∈R．
  （1）討論函數(shù)f（x）的單調(diào)性；
  （2）當(dāng)a＞0時(shí)，證明：f（x）≥

  2

  a

  -

  1

  a

  ．
  組卷：300引用：8難度：0.4

  解析

• 23．已知函數(shù)f（x）=（x-2）e^x．
  （1）求曲線y=f（x）在點(diǎn)（2，f（2））處的切線方程；
  （2）設(shè)g（x）=f（x）+lnx-x+2，記函數(shù)y=g（x）在（

  1

  2

  ，1）上的最大值為g（a）（a∈R），證明：g（a）＜-1．
  組卷：84引用：4難度：0.5

  解析