2022-2023學年福建省莆田五中高一（上）暑期返校數學試卷（一）

一、單選題

• 1．i為虛數單位，復數z滿足z（2-i）=i²⁰²²，則下列說法正確的是（　　）

  A．|z|= 1 5

  B． z =- 2 5 - 1 5 i

  C．z的虛部為- 1 5 i

  D．z在復平面內對應的點在第三象限
  組卷：102引用：4難度：0.8

  解析

• 2．設α，β滿足

  tan

  （

  α

  +

  3

  π

  4

  ）

  =

  3

  ，

  tan

  （

  β

  +

  π

  4

  ）

  =

  2

  ，則tan（α+β）=（　　）

  A．-1

  B． - 1 2

  C． 1 7

  D．1
  組卷：319引用：3難度：0.6

  解析

• 3．某科考試成績公布后，發現判錯一道題，經修改后重新公布，如表是抽取10名學生的成績，依據這些信息修改后的成績與修改前的相比，這10名學生成績的（　　）

  學生學號	1	2	3	4	5	6	7	8	9	10
  修改前成績	126	130	104	100	133	123	100	120	139	103
  修改后成績	126	135	99	100	138	123	95	120	144	98

  A．平均分、方差都變小	B．平均分、方差都變大
  C．平均分不變、方差變小	D．平均分不變、方差變大
  組卷：133引用：3難度：0.7

  解析

• 4．已知m,n是兩條不同的直線，α，β是兩個不同的平面，則下列判斷正確的是（　　）

  A．若m⊥α，n⊥β，α⊥β，則直線m與n可能相交或異面

  B．若α⊥β，m?α，n?β，則直線m與n一定垂直

  C．若m⊥α，n∥β，α⊥β，則直線m與n一定垂直

  D．若m∥α，n∥β，α∥β，則直線m與n一定平行
  組卷：52引用：2難度：0.6

  解析

• 5．若向量

  a

  ，

  b

  滿足|

  a

  |=|

  b

  |=2，

  |

  a

  +

  b

  |

  =

  2

  3

  ，則

  a

  -

  b

  在

  b

  上的投影向量為（　　）

  A． b

  B． 1 2 b

  C． - 1 2 b

  D． - b
  組卷：8引用：1難度：0.8

  解析

• 6．銳角△ABC的三個內角A，B，C所對的邊分別是a,b,c,某數學興趣小組探究該三角形時，提出以下四個論斷：甲：B＞C；乙：cosB＜cosC；丙：cosB＜sinC；丁：ccosB＜bcosC．若上述四個論斷中有且只有一個是正確的，則正確的是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  組卷：41引用：3難度：0.7

  解析

• 7．如圖是北京2022年冬奧會會徽的圖案，奧運五環的大小和間距如圖所示．若圓半徑均為12，相鄰圓圓心水平路離為26，兩排圓圓心垂直距離為11．設五個圓的圓心分別為O₁、O₂、O₃、O₄、O₅，則

  O

  4

  O

  1

  ?

  （

  O

  4

  O

  5

  +

  O

  4

  O

  2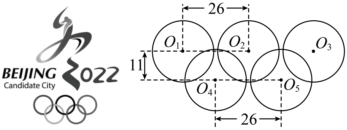

  ）

  的值為（　　）
  

  A．-507

  B．-386

  C．-338

  D．-242
  組卷：76引用：4難度：0.8

  解析

四、解答題

• 22．在平面四邊形ABCD中，點B，D在直線AC的兩側，AB=3，BC=5，四個內角分別用A，B，C，D表示，cosB=-cosD=

  3

  5

  ．
  （1）求∠BAC；
  （2）求△ABD與△ACD的面積之和的最大值．
  組卷：101引用：5難度：0.5

  解析

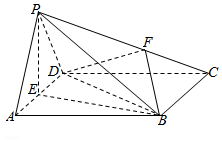• 23．如圖，在四棱錐P-ABCD中，底面ABCD是菱形，∠BAD=60°，△PAD是正三角形，E為線段AD的中點，

  PF

  =

  λ

  FC

  （

  λ

  ＞

  0

  ）

  ．
  （1）求證：平面PBC⊥平面PBE；
  （2）是否存在點F，使得

  V

  B

  -

  PAE

  =

  5

  8

  V

  D

  -

  PFB

  ？若存在，求出λ的值；若不存在，請說明理由．
  （3）若平面PAD⊥平面ABCD，在平面PBE內確定一點H，使CH+FH的值最小，并求此時

  BH

  BP

  的值．
  組卷：528引用：3難度：0.3

  解析