2022-2023學(xué)年江蘇省鹽城市阜寧中學(xué)銜接班高一（上）第一次學(xué)情調(diào)研數(shù)學(xué)試卷

一、單項(xiàng)選擇題：本大題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的，請(qǐng)把答案填涂在答題卡相應(yīng)位置上．

• 1．滿足{1，2，3}?A?{0，1，2，3，4，5}的集合A個(gè)數(shù)是（　　）

  A．5

  B．6

  C．7

  D．8
  組卷：139引用：3難度：0.9

  解析

• 2．函數(shù)

  f

  （

  x

  ）

  =

  （

  1

  2

  ）

  |

  x

  |

  -1的圖象大致為（　　）

  A．

  B．

  C．

  D．
  組卷：86引用：5難度：0.8

  解析

• 3．設(shè)

  a

  =

  3

  -

  1

  2

  ，

  b

  =

  （

  1

  2

  ）

  -

  1

  3

  ，c=log₂

  1

  3

  ，則（　　）

  A．a(chǎn)＜c＜b

  B．c＜a＜b

  C．b＜c＜a

  D．a(chǎn)＜b＜c
  組卷：131引用：5難度：0.8

  解析

• 4．已知a,b都為正實(shí)數(shù)，2a+b=1，則ab的最大值是（　　）

  A． 2 9

  B． 1 8

  C． 1 4

  D． 1 2
  組卷：472引用：9難度：0.7

  解析

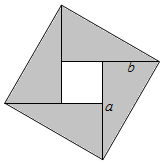• 5．三國(guó)時(shí)期趙爽所制的弦圖由四個(gè)全等的直角三角形構(gòu)成，如圖可用來(lái)解釋下列哪個(gè)命題（　　）

  A．如果a＞b,b＞c,那么a＞c

  B．如果a＞b＞0，那么a2＞b2

  C．對(duì)任意正實(shí)數(shù)a和b,有a2+b2≥2ab,當(dāng)且僅當(dāng)a=b時(shí)等號(hào)成立

  D．如果a＞b,c＞0，那么ac＞bc
  組卷：60引用：4難度：0.8

  解析

• 6．若A、B是全集I的真子集，則下列五個(gè)命題：①A∩B=A；②A∪B=A；③A∩（?_IB）=?；④A∪B=I；⑤x∈B是x∈A的必要不充分條件．其中與命題A?B等價(jià)的有（　　）

  A．1個(gè)

  B．2個(gè)

  C．3個(gè)

  D．4個(gè)
  組卷：28引用：1難度：0.7

  解析

• 7．若不等式mx²-4mx+3≠0對(duì)任意實(shí)數(shù)x均成立，則實(shí)數(shù)m的取值范圍是（　　）

  A． [ 0 ， 3 4 ）	B． （ 0 ， 3 4 ）
  C． [ 0 ， 3 4 ]	D． （ - ∞ ， 0 ） ∪ （ 3 4 ， + ∞ ）
  組卷：67引用：1難度：0.7

  解析

四、解答題（共6小題，滿分70分）

• 21．已知函數(shù)y=a^x（a＞0且a≠1）在[1，2]上最大值和最小值的和為12，令f（x）=

  a

  x

  a

  x

  +

  3

  ．
  （1）求實(shí)數(shù)a的值；
  （2）并探究f（x）+f（1-x）是否為定值，若是定值，寫(xiě)出證明過(guò)程；若不是定值，請(qǐng)說(shuō)明理由；
  （3）解不等式：f（1-x）+2f²（x）＜1．
  組卷：60引用：1難度：0.5

  解析

• 22．若函數(shù)f（x）在x∈[a,b]時(shí)，函數(shù)值y的取值區(qū)間恰為

  [

  1

  b

  ，

  1

  a

  ]

  ，就稱區(qū)間[a,b]為f（x）的一個(gè)“倒域區(qū)間”．定義在[-2，2]上的奇函數(shù)g（x），當(dāng)x∈[0，2]時(shí)，g（x）=-x²+2x.
  （1）求g（x）的解析式；
  （2）求函數(shù)g（x）在[1，2]內(nèi)的“倒域區(qū)間”；
  （3）若函數(shù)g（x）在定義域內(nèi)所有“倒域區(qū)間”上的圖像作為函數(shù)y=h（x）的圖像，是否存在實(shí)數(shù)m,使集合{（x,y）|y=h（x）}∩{（x,y）|y=x²+m}恰含有2個(gè)元素？若存在，求出m的值；若不存在，請(qǐng)說(shuō)明理由．
  組卷：99引用：4難度：0.3

  解析