滬教版高一（下）高考題同步試卷：6.3 函數y=Asin（ωx+φ）的圖像與性質（01）
發布：2024/12/19 2:30:2
一、選擇題（共18小題）
-
1．要得到函數y=sin（4x-
）的圖象，只需要將函數y=sin4x的圖象（ ）個單位．π3組卷：7691引用：99難度：0.9 -
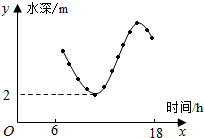2．如圖，某港口一天6時到18時的水深變化曲線近似滿足函數y=3sin（x+φ）+k.據此函數可知，這段時間水深（單位：m）的最大值為（ ）π6組卷：2604引用：35難度：0.9 -
3．為了得到函數y=sin（2x+1）的圖象，只需把y=sin2x的圖象上所有的點（ ）
組卷：2055引用：37難度：0.9 -
4．將函數y=sinx的圖象向左平移
個單位，得到函數y=f（x）的函數圖象，則下列說法正確的是（ ）π2組卷：2407引用：45難度：0.9 -
5．為了得到函數y=sin（x+1）的圖象，只需把函數y=sinx的圖象上所有的點（ ）
組卷：1232引用：21難度：0.9 -
6．設函數f（x）=cosωx（ω＞0），將y=f（x）的圖象向右平移
個單位長度后，所得的圖象與原圖象重合，則ω的最小值等于（ ）π3組卷：5792引用：76難度：0.9 -
7．若函數
是偶函數，則φ=（ ）f（x）=sinx+φ3（φ∈[0，2π]）組卷：1771引用：47難度：0.9 -
8．為得到函數
的圖象，只需將函數y=sin2x的圖象（ ）y=cos（2x+π3）組卷：9622引用：135難度：0.7 -
9．函數y=sin（2x+φ）的圖象沿x軸向左平移
個單位后，得到一個偶函數的圖象，則φ的一個可能的值為（ ）π8組卷：3003引用：115難度：0.9 -
10．若將函數y=tan（ωx+
）（ω＞0）的圖象向右平移π4個單位長度后，與函數y=tan（ωx+π6）的圖象重合，則ω的最小值為（ ）π6組卷：3365引用：65難度：0.9
三、解答題（共7小題）
-
29．已知函數f（x）=2sin（ωx），其中常數ω＞0．
（Ⅰ）令ω=1，判斷函數的奇偶性，并說明理由．F（x）=f（x）+f（x+π2）
（Ⅱ）令ω=2，將函數y=f（x）的圖象向左平移個單位，再向上平移1個單位，得到函數y=g（x）的圖象．對任意a∈R，求y=g（x）在區間[a,a+10π]上的零點個數的所有可能．π6組卷：1687引用：22難度：0.3 -
30．某同學用“五點法”畫函數f（x）=Asin（ωx+φ）（ω＞0，|φ|＜
）在某一個周期內的圖象時，列表并填入了部分數據，如表：π2
（1）請將上表數據補充完整，填寫在相應位置，并直接寫出函數f（x）的解析式；ωx+φ 0 π2π 3π22π x π35π6Asin（ωx+φ） 0 5 -5 0
（2）將y=f（x）圖象上所有點向左平行移動θ（θ＞0）個單位長度，得到y=g（x）的圖象．若y=g（x）圖象的一個對稱中心為（，0），求θ的最小值．5π12組卷：4284引用：50難度：0.5