2022-2023學年江蘇省鹽城市亭湖高級中學高三（上）摸底數(shù)學試卷

一、單選題

• 1．已知集合A={1，2，3，5，10}，B={x|x為質(zhì)數(shù)}，則A∩B的非空子集個數(shù)為（　　）

  A．4

  B．7

  C．8

  D．16
  組卷：63引用：4難度：0.8

  解析

• 2．已知命題p：?x≥1，lnx≥

  x

  +1，則?p為（　　）

  A． ? x ＜ 1 ， lnx ＜ x + 1	B． ? x ≥ 1 ， lnx ＜ x + 1
  C． ? x ≥ 1 ， lnx ≥ x + 1	D． ? x ＜ 1 ， lnx ＜ x + 1
  組卷：206引用：6難度：0.9

  解析

• 3．函數(shù)f（x）=ln（x²-2x-8）的單調(diào)遞增區(qū)間是（　　）

  A．（-∞，-2）

  B．（-∞，-1）

  C．（1，+∞）

  D．（4，+∞）
  組卷：11850引用：49難度：0.7

  解析

• 4．為了得到函數(shù)y=log₂（2x+2）的圖像，只需把函數(shù)y=log₂x的圖像上的所有點（　　）

  A．向左平移2個單位長度，再向上平移2個單位長度

  B．向右平移2個單位長度，再向下平移2個單位長度

  C．向左平移1個單位長度，再向上平移1個單位長度

  D．向右平移1個單位長度，再向下平移1個單位長度
  組卷：123引用：3難度：0.8

  解析

• 5．函數(shù)f（x）=（x-

  1

  x

  ）?ln|x|的圖象可能是（　　）

  A．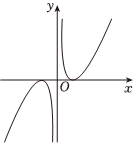

  B．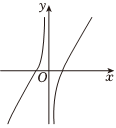

  C．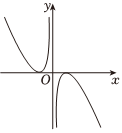

  D．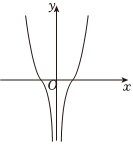
  組卷：40引用：3難度：0.7

  解析

• 6．已知函數(shù)f（x）是定義在R上的偶函數(shù)，且在（-∞，0]上是單調(diào)遞增的．設a=f（log₄5），b=f（log₄

  1

  3

  ），
  c=f（0.2^0.5），則a,b,c的大小關系為（　　）

  A．a(chǎn)＜b＜c

  B．c＜a＜b

  C．a(chǎn)＜c＜b

  D．b＜a＜c
  組卷：137引用：4難度：0.7

  解析

• 7．已知函數(shù)f（x）的定義域為R、且滿足：f（-x+2）=-f（x+2），又f（x+1）為偶函數(shù)，當x∈[0，2]時，f（x）=ax²+2x+b,則f（1）+f（3）+f（5）+f（7）的值為（　　）

  A．4

  B．-4

  C．0

  D．2
  組卷：124引用：1難度：0.6

  解析

四、解答題

• 21．已知函數(shù)

  f

  （

  x

  ）

  =

  2

  x

  -

  1

  2

  x

  +

  1

  ?．
  （1）判斷并證明f（x）?在其定義域上的單調(diào)性；
  （2）若f（k?3^x）+f（3^x-9^x+2）＜0?對任意x≥1?恒成立，求實數(shù)k?的取值范圍．
  組卷：164引用：7難度：0.5

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  2

  -

  2

  （

  a

  +

  1

  ）

  x

  +

  a

  -

  lnx

  ．
  （1）當a=1時，求f（x）的單調(diào)區(qū)間；
  （2）若0＜a＜1，設x₁，x₂是f（x）的兩個極值點，求證；

  f

  （

  x

  2

  ）

  -

  f

  （

  x

  1

  ）

  x

  2

  -

  x

  1

  ＜

  1

  a

  -

  2

  1

  +

  a

  ．
  組卷：74引用：4難度：0.3

  解析