2022-2023學(xué)年北京市順義二中高二（上）期中數(shù)學(xué)試卷

一、單選題（每個(gè)小題只有一項(xiàng)符合題意要求，請(qǐng)將所選答案前的字母按規(guī)定要求填涂在答題的相對(duì)位置上，每小題4分，本大題共10小題，共40.0分）

• 1．直線l經(jīng)過(guò)原點(diǎn)O和點(diǎn)A（1，-1），則直線l的傾斜角是（　　）

  A．45°

  B．135°

  C．45°或135°

  D．-45°
  組卷：328引用：5難度：0.8

  解析

• 2．在空間直角坐標(biāo)系中，若M（0，1，3），N（2，1，1），則

  MN

  =（　　）

  A．（-2，0，2）

  B．（2，0，-2）

  C．（2，2，0）

  D．（2，2，-1）
  組卷：147引用：4難度：0.7

  解析

• 3．從裝有3個(gè)紅球、2個(gè)白球的袋中任取2個(gè)球，則所取的2個(gè)球中至少有1個(gè)白球的概率是（　　）

  A． 1 10

  B． 3 10

  C． 7 10

  D． 3 5
  組卷：47引用：5難度：0.9

  解析

• 4．為了調(diào)查老師對(duì)微課堂的了解程度，某市擬采用分層抽樣的方法從A，B，C三所中學(xué)抽取60名教師進(jìn)行調(diào)查，已知A，B，C三所學(xué)校中分別有180，270，90名教師，則從C學(xué)校中應(yīng)抽取的人數(shù)為（　　）

  A．10

  B．12

  C．18

  D．24
  組卷：75引用：7難度：0.9

  解析

• 5．向量

  a

  =（-2，-3，1），

  b

  =（2，0，4），

  c

  =（-4，-6，2），下列結(jié)論正確的是（　　）

  A． a ∥ b ， a ∥ c

  B． a ∥ c ， a ⊥ b

  C． a ∥ b ， a ⊥ c

  D．以上都不對(duì)
  組卷：35引用：3難度：0.8

  解析

• 6．若直線l的方向向量為

  a

  =

  （

  2

  ，

  1

  ，

  m

  ）

  ，平面α的法向量為

  n

  =

  （

  1

  ，

  1

  2

  ，

  2

  ）

  ，且l∥a,則（　　）

  A． - 4 5

  B． - 5 4

  C．4

  D． 5 2
  組卷：197引用：8難度：0.8

  解析

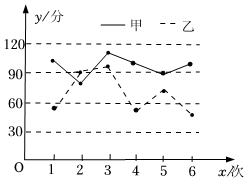• 7．已知甲、乙兩名同學(xué)在高三的6次數(shù)學(xué)測(cè)試的成績(jī)統(tǒng)計(jì)如圖，則下列說(shuō)法不正確的是（　　）

  A．若甲、乙兩組數(shù)據(jù)的平均數(shù)分別為 x 1 ， x 2 ，則 x 1 ＞ x 2

  B．若甲、乙兩組數(shù)據(jù)的方差分別為 s 2 1 ， s 2 2 ，則 s 2 1 ＞ s 2 2

  C．甲成績(jī)的極差小于乙成績(jī)的極差

  D．甲成績(jī)比乙成績(jī)穩(wěn)定
  組卷：122引用：3難度：0.7

  解析

三、解答題（本大題共6小題，共85.0分）

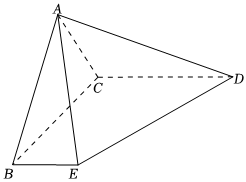• 20．如圖，在四棱錐A-BCDE中，平面ABC⊥平面BCDE，AB=AC=CD=2BE=2，BE∥CD，CD⊥CB，AB⊥AC，O為BC中點(diǎn)．
  （1）求直線AE與BC所成角的余弦值；
  （2）點(diǎn)B到平面ADE的距離；
  （3）線段AC上是否存在一點(diǎn)Q，使OQ∥平面ADE？如果不存在，請(qǐng)說(shuō)明理由；如果存在，求

  AQ

  AC

  的值．
  組卷：137引用：1難度：0.5

  解析

• 21．在梯形ABCD中，AB∥CD，∠BAD=60°，AB=2AD=2CD=4，P為AB的中點(diǎn)，線段AC與DP交于O點(diǎn)，將△ACD沿AC折起到△ACD'的位置，使得平面ACB⊥平面ACD'．
  
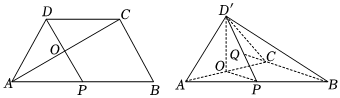
  （1）求證：BC∥平面POD'；
  （2）平面ABC與平面BCD'夾角的余弦值；
  （3）線段PD'上是否存在點(diǎn)Q，使得CQ與平面BCD'所成角的正弦值為

  6

  8

  ？若存在，求出

  PQ

  PD

  ′

  的值：若不存在，請(qǐng)說(shuō)明理由．
  組卷：85引用：3難度：0.5

  解析