2022-2023學年廣東省深圳市羅湖外語學校初中部九年級（上）段考數學試卷（11月份）

一、選擇題（每小題3分，共30分）

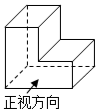• 1．如圖所示的幾何體的俯視圖是（　　）

  A．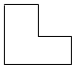

  B．

  C．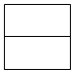

  D．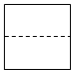
  組卷：350引用：5難度：0.9

  解析

• 2．在Rt△ABC中，∠C=90°，BC=4，AC=3，則sinA的值是（　　）

  A． 4 5

  B． 3 5

  C． 4 3

  D． 5 4
  組卷：224引用：1難度：0.7

  解析

• 3．對于反比例函數

  y

  =

  -

  3

  x

  ，下列說法不正確的是（　　）

  A．圖象經過點（1，-3）

  B．圖象分布在第二、四象限

  C．點A（x1，y1），B（x2，y2）都在反比例函數 y = - 3 x 的圖象上，若x1＜x2，則y1＜y2

  D．當x＞0時，y隨x的增大而增大
  組卷：158引用：2難度：0.6

  解析

• 4．如圖，菱形ABCD的對角線AC，BD相交于O點，E，F分別是AB，BC邊上的中點，連接EF．若EF=2

  √

  3

  ，BD=8，則菱形ABCD的周長為（　　）

  A．8

  B．8 √ 6

  C．16 √ 3

  D．8 √ 7
  組卷：224引用：8難度：0.7

  解析

• 5．下列命題，其中是真命題的是（　　）

  A．對角線互相垂直的四邊形的中點四邊形是菱形

  B．有一個角是直角的四邊形是矩形

  C．對角線互相平分的平行四邊形是菱形

  D．對角線互相垂直的矩形是正方形
  組卷：101引用：3難度：0.6

  解析

• 6．新冠肺炎是一種傳染性極強的疾病，如果有一人患病，經過兩輪傳染后有64人患病，設每輪傳染中平均一個人傳染了x個人，下列列式正確的是（　　）

  A．x+x（1+x）=64	B．1+x+x2=64
  C．（1+x）2=64	D．x（1+x）=64
  組卷：1256引用：11難度：0.6

  解析

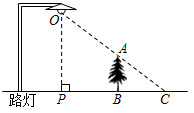• 7．如圖，小樹AB在路燈O的照射下形成投影BC．若樹高AB=2m,樹影BC=3m,樹與路燈的水平距離BP=4.5m.則路燈的高度OP為（　　）

  A．3m

  B．4m

  C．4.5m

  D．5m
  組卷：2254引用：27難度：0.5

  解析

三、解答題（本大題共7小題，其中第16題6分，第17題7分，第18題6分，第19題8分，第20題8分，第21題10分，第22題10分，共55分）

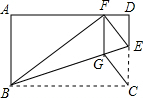• 21．如圖，矩形ABCD中，點E在邊CD上，將△BCE沿BE折疊，點C落在AD邊上的點F處，過點F作FG∥CD交BE于點G，連接CG．
  （1）求證：四邊形CEFG是菱形；
  （2）若AB=6，AD=10，求四邊形CEFG的面積．
  組卷：5428引用：45難度：0.5

  解析

• 22．如圖1，已知點G在正方形ABCD的對角線AC上，GE⊥BC，垂足為點E，GF⊥CD，垂足為點F．
  
  （1）推斷：

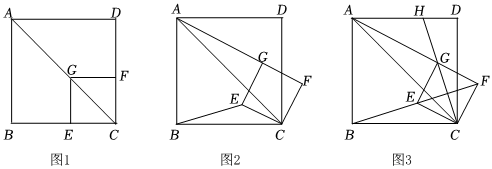
  AG

  BE

  的值為

  ；（直接寫出結果）
  （2）探究與證明：將正方形CEGF繞點C順時針方向旋轉α角（0＜α＜45°），如圖2所示，試探究線段AG與BE之間的數量關系，并說明理由；
  （3）拓展與運用：正方形CEGF在旋轉過程中，當B，E，F三點在一條直線上時，如圖3所示，延長CG交AD于點H．若AG=6，

  GH

  =

  2

  √

  2

  ，則BC=

  ．
  組卷：230引用：2難度：0.1

  解析