2021-2022學年湖北省部分重點學校高二（上）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知直線l經過A（1，3），B（-2，4）兩點，則直線l的斜率是（　　）

  A． 1 3

  B．- 1 3

  C．3

  D．-3
  組卷：235引用：9難度：0.7

  解析

• 2．直線

  3

  x

  -

  y

  +

  1

  =

  0

  和直線

  y

  =

  3

  x

  +

  3

  之間的距離為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：46引用：2難度：0.8

  解析

• 3．某同學做立定投籃訓練，共兩場，第一場投籃20次的命中率為80%，第二場投籃30次的命中率為70%，則該同學這兩場投籃的命中率為（　　）

  A．72%

  B．74%

  C．75%

  D．76%
  組卷：181引用：2難度：0.7

  解析

• 4．已知點A（-2，0），B（0，2），則以線段AB為直徑的圓的標準方程為（　　）

  A．（x+1）2+（y-1）2=8	B．（x-1）2+（y+1）2=8
  C．（x+1）2+（y-1）2=2	D．（x-1）2+（y+1）2=2
  組卷：82引用：3難度：0.8

  解析

• 5．某民族學校有92%的學生喜歡民歌或民舞，62%的學生喜歡民歌，80%的學生喜歡民舞，則該學校既喜歡民歌又喜歡民舞的學生數占該校學生總數的比例是（　　）

  A．48%

  B．50%

  C．52%

  D．60%
  組卷：11引用：1難度：0.7

  解析

• 6．已知在圓C：（x-a）²+（y-2a）²=20上恰有兩個點到原點的距離為

  5

  ，則a的取值范圍是（　　）

  A．（1，3）	B．（1，9）
  C．（-3，-1）∪（1，3）	D．（-9，-1）∪（1，9）
  組卷：405引用：5難度：0.5

  解析

• 7．在三棱柱ABC-A₁B₁C₁中，E是棱AC的三等分點，且AC=3AE，F是棱B₁C₁的中點，若

  AB

  =

  a

  ，

  AC

  =

  b

  ，

  A

  A

  1

  =

  c

  ，則

  EF

  =（　　）

  A． 1 2 a - 1 6 b + c

  B． 1 3 a + 1 6 b + c

  C． 1 3 a - 1 6 b + c

  D． 1 2 a + 1 6 b + c
  組卷：160引用：9難度：0.8

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

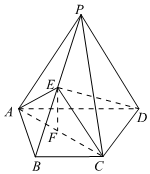• 21．如圖，在四棱錐P-ABCD中，四邊形ABCD是等腰梯形，且AD=2AB=2BC=2CD，E，F分別是線段PB，AC的中點，PA=PD，平面PAD⊥平面ABCD．
  （1）證明：EF⊥平面ABCD．
  （2）求平面ACE與平面ADE所成銳二面角的取值范圍．
  組卷：79引用：2難度：0.5

  解析

• 22．已知圓C的圓心C在直線x+y-4=0上，且圓C經過M（2，0），N（0，2）兩點．
  （1）求圓C的方程；
  （2）已知點P（0，m），過原點的直線l與圓C交于A，B兩點，且PA⊥PB．若1＜m＜3，求直線l的斜率k的取值范圍．
  組卷：198引用：2難度：0.3

  解析