2018-2019學(xué)年北京市海淀區(qū)清華附中九年級(jí)（下）開學(xué)數(shù)學(xué)試卷

一、選擇題（本題共16分，每題2分）

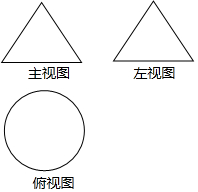• 1．如圖是某幾何圖形的三視圖，則這個(gè)幾何圖形是（　　）

  A．圓柱

  B．正方體

  C．三棱錐

  D．圓錐
  組卷：81引用：1難度：0.8

  解析

• 2．實(shí)數(shù)a,b,c在數(shù)軸上的對(duì)應(yīng)點(diǎn)的位置如圖所示，則正確的結(jié)論是（　　）

  A．a(chǎn)+c＞0

  B．a(chǎn)-b＞0

  C．|a|＞|c|

  D．bc＞0
  組卷：240引用：2難度：0.7

  解析

• 3．下列圖形中，是中心對(duì)稱圖形的是（　　）

  A．

  B．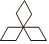

  C．

  D．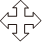
  組卷：603引用：20難度：0.7

  解析

• 4．使分式

  x

  x

  -

  1

  有意義的x的取值范圍是（　　）

  A．x≥1

  B．x≤1

  C．x＞1

  D．x≠1
  組卷：1160引用：20難度：0.9

  解析

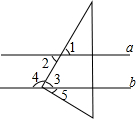• 5．如圖，已知a∥b,直角三角板的直角頂點(diǎn)在直線b上，若∠1=60°，則下列結(jié)論錯(cuò)誤的是（　　）

  A．∠2=60°

  B．∠3=60°

  C．∠4=120°

  D．∠5=40°
  組卷：2492引用：31難度：0.7

  解析

• 6．在做“拋擲一枚質(zhì)地均勻的硬幣”實(shí)驗(yàn)時(shí)，下列說法正確的是（　　）

  A．隨著拋擲的次數(shù)增加，“正面朝上”的頻率越來越小

  B．不同次數(shù)的實(shí)驗(yàn)，“正面朝上”的頻率可能會(huì)不相同

  C．當(dāng)拋擲的次數(shù)很大時(shí)，“正面朝上”的次數(shù)一定占總拋擲次數(shù)的 1 2

  D．連續(xù)拋擲3次硬幣都是正面朝上，第4次拋出現(xiàn)“正面朝上”的概率小于 1 2
  組卷：83引用：1難度：0.7

  解析

• 7．為了測(cè)量被池塘隔開的A，B兩點(diǎn)之間的距離，根據(jù)實(shí)際情況，作出如圖所示的圖形，其中AB⊥BE，EF⊥BE，AF交BE于點(diǎn)D，C在BD上，有四位同學(xué)分別測(cè)量出以下四組數(shù)據(jù)：①BC，∠ACB；②CD，∠ACB，∠ADB；③EF，DE，BD；④DE，DC，BC．能根據(jù)所測(cè)數(shù)據(jù)，求出A、B間距離的有（　　）

  A．4組

  B．3組

  C．2組

  D．1組
  組卷：128引用：4難度：0.7

  解析

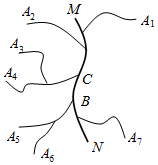• 8．如圖，在公路MN兩側(cè)分別有A₁，A₂…A₇，七個(gè)工廠，各工廠與公路MN（圖中粗線）之間有小公路連接．現(xiàn)在需要在公路MN上設(shè)置一個(gè)車站，選擇站址的標(biāo)準(zhǔn)是“使各工廠到車站的距離之和越小越好”．則下面結(jié)論中正確的是（　　）
  ①車站的位置設(shè)在C點(diǎn)好于B點(diǎn)；
  ②車站的位置設(shè)在B點(diǎn)與C點(diǎn)之間公路上任何一點(diǎn)效果一樣；
  ③車站位置的設(shè)置與各段小公路的長(zhǎng)度無關(guān)．

  A．①

  B．②

  C．①③

  D．②③
  組卷：647引用：6難度：0.5

  解析

二、填空題奔向（本題共16分，每小題2分）

• 9．分解因式：x²-9y²

   

  ．
  組卷：719引用：119難度：0.7

  解析

三、解答題（本題共68分，第17-22題，每小題5分，第23-26題，每小題5分，第27、28題，每小題5分）

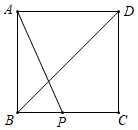• 27．已知，點(diǎn)P在正方形ABCD的邊BC上，過點(diǎn)P作垂直于AP的直線l,過點(diǎn)C作平行于BD的直線m,直線l與直線n相交于點(diǎn)Q，連接AQ交BD于點(diǎn)E，連接PE
  （1）依題意補(bǔ)全圖形；
  （2）求證：PA=PQ；
  （3）探究線段AB，BP，PE之間的數(shù)量關(guān)系，并給予證明．
  組卷：145引用：1難度：0.6

  解析

• 28．如果在圖形M上存在兩個(gè)不同的點(diǎn)S，T，使得∠SPT=90°，則稱點(diǎn)P為圖形M的“友好點(diǎn)”．在平面直角坐標(biāo)系xOy中，A（-2，0），B（2，0），C（0，2

  3

  ）
  （1）點(diǎn)H（1，1），I（2，1），J（

  3

  ，1）中，線段AB的“友好點(diǎn)”的有

  ．
  （2）在直線y=

  3

  x+b上存在線段BC的“友好點(diǎn)”，求實(shí)數(shù)b的取值范圍；
  （3）如果點(diǎn)D在直線y=

  3

  x上，⊙D的半徑為1，若⊙D上存在△ABC的“友好點(diǎn)”，求點(diǎn)D的橫坐標(biāo)的取值范圍．
  組卷：94引用：1難度：0.1

  解析