2021-2022學(xué)年遼寧省鞍山三中高一（下）期末數(shù)學(xué)試卷

一、單選題：本題共8小題，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)符合題目要求。

• 1．i是虛數(shù)單位，計(jì)算

  2

  1

  +

  3

  i

  的結(jié)果為（　　）

  A． 1 5 - 3 5 i

  B． - 1 5 + 3 5 i

  C． 1 4 - 3 4 i

  D． - 1 4 + 3 4 i
  組卷：209引用：5難度：0.8

  解析

• 2．已知θ是第四象限角，且

  sinθ

  =

  -

  3

  5

  ，則

  tan

  （

  θ

  -

  π

  4

  ）

  =（　　）

  A． 1 7

  B．-7

  C． - 1 7

  D．7
  組卷：257引用：5難度：0.5

  解析

• 3．下列命題正確的是（　　）

  A．若 a = （ - 1 ， 2 ） ， b = （ m 2 ， 1 ） ，且 a ⊥ b ，則 m = 2

  B．若 ? λ ∈ R ， a ≠ λ b ，則 a ， b 不共線

  C．若 OB ， OC 是平面內(nèi)不共線的向量，且存在實(shí)數(shù)y使得 OA + y OC = y OB + OC ，則A，B，C三點(diǎn)共線

  D．若 a = （ - 1 ， 1 ） ， b = （ 1 ， 2 ） ，則 b 在 a 上的投影向量為 （ 1 2 ，- 1 2 ）
  組卷：65引用：5難度：0.6

  解析

• 4．設(shè)α，β，γ為三個(gè)平面，l,m,n為三條直線，則下列說(shuō)法不正確的是（　　）

  A．若m?α，l∥m,則l∥α

  B．若l上有兩點(diǎn)到α的距離相等，則l∥α

  C．α，β，γ兩兩相交于三條直線l,m,n,若l∥m,則n∥m

  D．若m?α，n?α，m∥β，n∥β，則α∥β
  組卷：137引用：4難度：0.7

  解析

• 5．若α∈（0，π），

  sinα

  +

  cosα

  =

  1

  2

  ，則cos2α=（　　）

  A． 7 4

  B． - 7 4

  C． 3 4

  D． - 3 4
  組卷：350引用：1難度：0.8

  解析

• 6．已知菱形ABCD邊長(zhǎng)為8，∠BAD=60°，對(duì)角線AC與BD交于點(diǎn)O，將菱形ABCD沿對(duì)角線BD翻折成平面角為θ的二面角，若θ∈[90°，120°]，則翻折后點(diǎn)O到直線AC距離的取值范圍為（　　）

  A．[ 3 ， 2 6 ]

  B．[ 2 3 ， 2 6 ]

  C．[ 2 3 ， 3 6 ]

  D．[ 3 ， 3 6 ]
  組卷：90引用：2難度：0.6

  解析

• 7．在△ABC中，已知角A，B，C所對(duì)的邊分別為a,b,c,若

  asin

  B

  +

  bcos

  A

  =

  2

  b

  ．D為線段BC的中點(diǎn)，且

  AD

  =

  7

  ，

  BC

  =

  2

  5

  ，則△ABC的面積為（　　）

  A． 2

  B． 2 2

  C． 2 3

  D．1
  組卷：300引用：3難度：0.5

  解析

三、解答題：本題共6道小題，共70分。

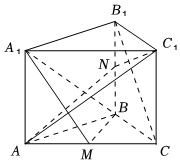• 21．如圖，在直三棱柱ABC-A₁B₁C₁中，M為棱AC的中點(diǎn)，AB=BC，AC=2，AA₁=

  2

  ．
  （1）求證：B₁C∥平面A₁BM；
  （2）求證：AC₁⊥平面A₁BM；
  （3）在棱BB₁上是否存在點(diǎn)N，使得平面AC₁N⊥平面AA₁C₁C？如果存在，求此時(shí)

  BN

  B

  B

  1

  的值；如果不存在，請(qǐng)說(shuō)明理由．
  組卷：412引用：7難度：0.6

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  4

  sinxsin

  （

  x

  +

  π

  6

  ）

  +

  1

  -

  3

  ．
  （1）若關(guān)于x的方程f（x）+m-

  3

  =0在

  x

  ∈

  [

  π

  3

  ，

  π

  2

  ]

  上有解，求實(shí)數(shù)m的取值范圍；
  （2）記△ABC的內(nèi)角B滿足

  f

  （

  B

  2

  ）

  =

  1

  ，

  AC

  邊上的高BD為2，求

  2

  BC

  +

  1

  AB

  的最大值；
  （3）函數(shù)f（x）的圖象縱坐標(biāo)不變，橫坐標(biāo)伸長(zhǎng)為原來(lái)的4倍，再把整個(gè)圖象向左平移

  2

  π

  3

  個(gè)單位長(zhǎng)度，再將函數(shù)圖像向下平移1個(gè)單位得到g（x）的圖象．若M（π-2，3），N（π+2，6），問(wèn)在y=g（x）的圖象上是否存在一點(diǎn)P，使得

  MP

  ⊥

  NP

  ．若存在，求出P點(diǎn)坐標(biāo)；若不存在，說(shuō)明理由．
  組卷：130引用：2難度：0.5

  解析