當(dāng)前位置：試卷中心 > 試卷詳情

2022-2023學(xué)年湖南省長(zhǎng)沙市雅禮中學(xué)高二（下）第一次月考數(shù)學(xué)試卷（3月份）

發(fā)布：2024/4/20 14:35:0

1．設(shè)復(fù)數(shù)z滿足（1+i）z=2i,則|z|=（　　）
A．
1
2
B．
2
2
C．
2
D．2
組卷：5981引用：62難度：0.9
解析
2．記S_n為等差數(shù)列{a_n}的前n項(xiàng)和．若a₄+a₅=24，S₆=48，則{a_n}的公差為（　　）
A．1 B．2 C．4 D．8
組卷：15417引用：82難度：0.7
解析
3．函數(shù)f（x）=
sinx
+
x
cosx
+
x
2
在[-π，π]的圖象大致為（　　）
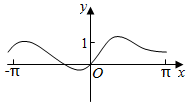
A． B．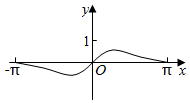
C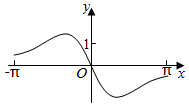． D．
組卷：9656引用：52難度：0.8
解析
4．
a
，
b
是兩個(gè)向量，|
a
|=1，|
b
|=2，且（
a
+
b
）⊥
a
，則
a
與
b
的夾角為（　　）
A．30° B．60° C．120° D．150°
組卷：72引用：23難度：0.7
解析
5．（x-2y）（2x-y）⁵的展開(kāi)式中的x³y³系數(shù)為（　　）
A．-200 B．-120 C．120 D．200
組卷：225引用：10難度：0.8
解析
6．已知橢圓E：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的右焦點(diǎn)為F（3，0），過(guò)點(diǎn)F的直線交橢圓于A，B兩點(diǎn)，若AB的中點(diǎn)坐標(biāo)為（1，-1），則E的方程為（　　）
A．
x
2
18
+
y
2
9
=
1
B．
x
2
27
+
y
2
18
=
1
C．
x
2
36
+
y
2
27
=
1
D．
x
2
45
+
y
2
36
=
1
組卷：1095引用：30難度：0.7
解析
7．已知
sin
（
α
-
π
6
）
+
cosα
=
3
5
，則
cos
（
2
α
+
π
3
）
=（　　）
A．
-
7
25
B．
7
25
C．
-
24
25
D．
24
25
組卷：1097引用：16難度：0.7
解析

21．設(shè)拋物線C：y²=2px（p＞0）的焦點(diǎn)為F，點(diǎn)D（p,0），過(guò)F的直線交C于M，N兩點(diǎn)．當(dāng)直線MD垂直于x軸時(shí)，|MF|=3．
（1）求C的方程；
（2）設(shè)直線MD，ND與C的另一個(gè)交點(diǎn)分別為A，B，記直線MN，AB的傾斜角分別為α，β．當(dāng)α-β取得最大值時(shí)，求直線AB的方程．
組卷：5823引用：10難度：0.3
解析
22．已知函數(shù)f（x）=
a
2
x
2
-x+lnx.
（Ⅰ）若函數(shù)f（x）在定義域內(nèi)是增函數(shù)，求實(shí)數(shù)a的取值范圍；
（Ⅱ）當(dāng)a∈[1，e）時(shí)，討論方程f（x）=ax-
a
2
根的個(gè)數(shù)．
組卷：183引用：5難度：0.3
解析

A． x 2 18 + y 2 9 = 1	B． x 2 27 + y 2 18 = 1
C． x 2 36 + y 2 27 = 1	D． x 2 45 + y 2 36 = 1

1．設(shè)復(fù)數(shù)z滿足（1+i）z=2i,則|z|=（ ）