2022-2023學年廣東省惠州市高二（上）期末數學試卷

一、單項選擇題：本題共8小題，每小題滿分40分，共40分.在每小題給出的四個選項中，只有一項符合題目要求，選對得5分，選錯得0分.

• 1．過點P（-1，3）且平行于直線x-2y+3=0的直線方程為（　　）

  A．2x+y-1=0

  B．2x+y-5=0

  C．x+2y-5=0

  D．x-2y+7=0
  組卷：178引用：11難度：0.9

  解析

• 2．已知{a_n}是等差數列，且a₂+1是a₁和a₄的等差中項，則{a_n}的公差為（　　）

  A．1

  B．2

  C．-2

  D．-1
  組卷：451引用：3難度：0.8

  解析

• 3．棱長為1的正四面體ABCD中，則

  AD

  ?

  BC

  等于（　　）

  A．0

  B． 1 2

  C． 1 4

  D． - 1 4
  組卷：123引用：2難度：0.9

  解析

• 4．已知橢圓C的一個焦點為（1，0），且過點

  （

  0

  ，

  3

  ）

  ，則橢圓C的標準方程為（　　）

  A． x 2 2 + y 2 3 = 1

  B． x 2 4 + y 2 3 = 1

  C． x 2 3 + y 2 2 = 1

  D． x 2 3 + y 2 4 = 1
  組卷：466引用：5難度：0.8

  解析

• 5．已知空間向量

  a

  =

  （

  2

  ，

  1

  ，-

  3

  ）

  ，則向量

  a

  在坐標平面xOy上的投影向量是（　　）

  A．（0，2，1）

  B．（2，1，0）

  C．（0，1，-3）

  D．（2，0，-3）
  組卷：557引用：3難度：0.9

  解析

• 6．已知直線l：2mx+y-m-1=0與圓C：x²+（y-2）²=4交于A，B兩點，則當弦AB最短時直線l的方程為（　　）

  A．2x-4y+3=0

  B．x-4y+3=0

  C．2x+4y+3=0

  D．2x+4y+1=0
  組卷：932引用：14難度：0.8

  解析

• 7．已知直線l₁的方程是y=mx+n,l₂的方程是y=nx-m（mn≠0，m≠n），則下列各圖形中，正確的是（　　）

  A．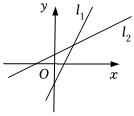

  B．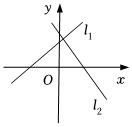

  C．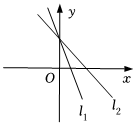

  D．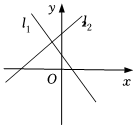
  組卷：463引用：7難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

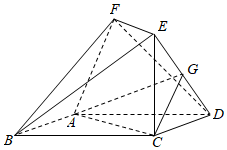• 21．如圖，在多面體ABCDEF中，四邊形ABCD是菱形，EF∥AC，EF=1，∠ABC=60°，CE⊥平面ABCD，

  CE

  =

  3

  ，CD=2，G是DE的中點．
  （1）求證：平面ACG∥平面BEF；
  （2）求直線AD與平面ABF所成的角的正弦值．
  組卷：227引用：9難度：0.5

  解析

• 22．已知雙曲線

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的右焦點為F（2，0），O為坐標原點，雙曲線C的兩條漸近線的夾角為

  π

  3

  ．
  （1）求雙曲線C的方程；
  （2）過點F作直線l交C于P，Q兩點，在x軸上是否存在定點M，使

  MP

  ?

  MQ

  為定值？若存在，求出定點M的坐標及這個定值；若不存在，說明理由．
  組卷：335引用：5難度：0.3

  解析