2020-2021學年遼寧省沈陽市五校協作體高一（下）期末數學試卷

一、單選題（共8小題，每小題5分，共計40分）

• 1．已知復數

  z

  =

  5

  i

  2

  -

  i

  +

  5

  i

  ，則|z|=（　　）

  A． 5

  B． 5 2

  C． 3 2

  D． 2 5
  組卷：431引用：15難度：0.8

  解析

• 2．密位制是度量角的一種方法．將周角等分為6000份，每一份叫做1密位的角．以密位作為角的度量單位，這種度量角的單位制，叫做角的密位制．在角的密位制中，采用四個數碼表示角的大小，單位名稱密位二字可以省去不寫．密位的寫法是在百位數字與十位數字之間畫一條短線，如：478密位寫成“4-78”，1周角等于6000密位，記作1周角=60-00．如果一個扇形的半徑為2，面積為

  7

  3

  π

  ，則其圓心角可以用密位制表示為（　　）

  A．25-00

  B．35-00

  C．42-00

  D．70-00
  組卷：172引用：6難度：0.8

  解析

• 3．已知角α的終邊繞原點O逆時針旋轉

  π

  2

  后，得到角β的終邊，角β的終邊過點P（8，-m），且cosβ=

  24

  5

  m

  ，則tanα的值為（　　）

  A．± 3 4

  B．- 3 4

  C．- 4 3

  D． 4 3
  組卷：280引用：3難度：0.6

  解析

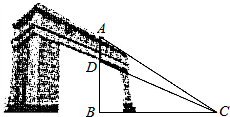• 4．某大學的大門蔚為壯觀，有個學生想搞清楚門洞拱頂D到其正上方A點的距離，他站在地面C處，利用皮尺量得BC=9米，利用測角儀測得仰角∠ACB=45°，測得仰角∠BCD后通過計算得到sin∠ACD=

  26

  26

  ，則AD的距離為（　　）

  A．2米

  B．2.5米

  C．3米

  D．4米
  組卷：79引用：3難度：0.7

  解析

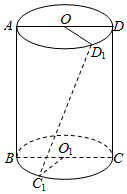• 5．如圖，矩形ABCD是圓柱OO₁的軸截面，且AB=

  3

  ，

  BC

  =

  2

  ，

  ?

  DD

  1

  =

  π

  3

  ，

  ?

  CC

  1

  =

  2

  3

  π，其中C₁，D₁在平面ABCD同側，則異面直線CD與C₁D₁所成的角為（　　）

  A．30°

  B．45°

  C．60°

  D．75°
  組卷：184引用：6難度：0.5

  解析

• 6．在直三棱柱ABC-A₁B₁C₁中，M是BB₁上的點，AB=3，BC=4，AC=5，CC₁=7，過三點A、M、C₁作截面，當截面周長最小時，截面將三棱柱分成的兩部分的體積比為（　　）

  A． 3 4

  B． 4 5

  C． 9 10

  D． 10 11
  組卷：72引用：1難度：0.6

  解析

• 7．將函數

  f

  （

  x

  ）

  =

  6

  cos

  （

  π

  4

  x

  ）

  和直線g（x）=x-2的所有交點從左到右依次記為A₁，A₂，…，A₅，若P點坐標為

  （

  0

  ，

  2

  3

  ）

  ，則

  |

  P

  A

  1

  +

  P

  A

  2

  +

  ?

  +

  P

  A

  5

  |

  =（　　）

  A．0

  B．4

  C．12

  D．20
  組卷：201引用：2難度：0.5

  解析

四、解答題

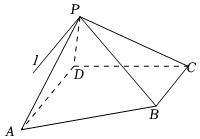• 21．如圖，四棱錐P-ABCD中，AD∥BC，平面PAD⊥平面PBC，且平面PAD∩平面PBC=l,

  ∠

  PBC

  =

  π

  2

  ．
  （1）證明：

  ∠

  APB

  =

  π

  2

  ；
  （2）若AD=CD=2BC=2PD=2，

  ∠

  BCD

  =

  π

  3

  ，求直線BD與平面PBC所成角的正弦值．
  組卷：78引用：2難度：0.5

  解析

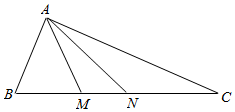• 22．如圖，直角△ABC中，點M，N在斜邊BC上（M，N異于B，C，且N在M，C之間），AB=3，

  AC

  =

  3

  3

  ，

  ∠

  MAN

  =

  π

  6

  ，設∠BAM=θ．
  （1）若

  sinθ

  =

  21

  7

  ，求MN的長；
  （2）求△AMN面積的最小值．
  組卷：58引用：1難度：0.5

  解析