2021-2022學年浙江省寧波市海曙區儲能中學九年級（下）起始考數學試卷

一、選擇題（本題有10小題，每小題4分，共40分）

• 1．下列事件中，屬于必然事件的為（　　）

  A．打開電視機，正在播放廣告

  B．任意畫一個三角形，它的內角和等于180°

  C．擲一枚硬幣，正面朝上

  D．在只有紅球的盒子里摸到白球
  組卷：634引用：6難度：0.5

  解析

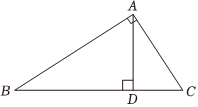• 2．如圖，在Rt△ABC中，∠BAC=90°，AD⊥BC于點D，則下列結論不正確的是（　　）

  A． sin B = AD AB

  B． sin B = AC BC

  C． sin B = AD AC

  D． sin B = CD AC
  組卷：7106引用：30難度：0.9

  解析

• 3．下列平面圖形中不能圍成正方體的是（　　）

  A．

  B．

  C．

  D．
  組卷：277引用：7難度：0.7

  解析

• 4．矩形ABCD中，AB=8，BC=3

  5

  ，點P在邊AB上，且BP=3AP，如果圓P是以點P為圓心，PD為半徑的圓，那么下列判斷正確的是（　　）

  A．點B，C均在圓P外

  B．點B在圓P外，點C在圓P內

  C．點B在圓P內，點C在圓P外

  D．點B，C均在圓P內
  組卷：1728引用：12難度：0.6

  解析

• 5．已知正方形ABCD，E是CD的中點，P是BC邊上的一點，下列條件中不能推出△ABP與△ECP相似的是（　　）

  A．∠APB=∠EPC	B．AB?PC=EC?BP
  C．P是BC的中點	D．BP：BC=2：3
  組卷：40引用：6難度：0.6

  解析

• 6．函數y=ax²+bx+3，當x=1與x=2021時，函數值相等，則當x=2022時，函數值等于（　　）

  A．-3

  B．- 3 2

  C． 3 2

  D．3
  組卷：293引用：2難度：0.6

  解析

• 7．如圖，在四邊形ABCD中，AB∥CD，AB=CD，∠B=60°，AD=8

  3

  ，分別以B和C為圓心，以大于

  1

  2

  BC的長為半徑作弧，兩弧相交于點P和Q，直線PQ與BA延長線交于點E，連接CE，則△BCE的內切圓半徑是（　　）

  A．4

  B．4 3

  C．2

  D．2 3
  組卷：604引用：4難度：0.5

  解析

• 8．如圖是某商品標牌的示意圖，⊙O與等邊△ABC的邊BC相切于點C，且⊙O的直徑與△ABC的高相等，已知等邊△ABC邊長為4，設⊙O與AC相交于點E，則AE的長為（　　）

  A． 3

  B．1

  C． 3 -1

  D． 3 2
  組卷：549引用：4難度：0.7

  解析

三.解答題（第17題6分，第18題8分，第19，20，22，23題每題10分，第21題12分，第24題14分，共80分）

• 23．在“童博會”上，某影樓為了積聚人氣，增加銷量，將“喜洋洋”套系進行降價促銷，已知這種套系的成本為400元/套．促銷方案如下：若團購3套，則可享受團購價680元/套．若團購每增加一套，則每套再降價50元，設某團團購的數量增加了x套．
  （1）填空：該團的團購數量為

  套；每套的利潤為

  元．（用含x的代數式表示）
  （2）規定一個團的團購數量不超過8套，當團購數量為多少套時，影樓獲得利潤最大？最大利潤為多少？
  組卷：73引用：1難度：0.5

  解析

• 24．如圖Rt△ABC中，∠ABC=90°，P是斜邊AC上一個動點，以BP為直徑作⊙O交BC于點D，與AC的另一個交點E，連接DE．
  （1）當

  ?

  DP

  =

  ?

  EP

  時，
  ①若

  ?

  BD

  =130°，求∠C的度數；
  ②求證AB=AP；
  （2）當AB=15，BC=20時，是否存在點P，使得△BDE是等腰三角形，若存在，求出所有符合條件的CP的長．
  
  組卷：261引用：3難度：0.4

  解析