2022年天津市河西區新華中學高考數學統練試卷（4月份）

一、選擇題。（本大題共9小題，每小題5分，共45分）

• 1．已知集合A={x|ln（x-1）＜0}，B={x|x²-3x+2≤0}，則A∩B=（　　）

  A．{x|1≤x＜2}

  B．{x|1≤x≤2}

  C．{x|1＜x≤2}

  D．{x|1＜x＜2}
  組卷：167引用：7難度：0.8

  解析

• 2．已知a∈R，則“a＞1”是“

  1

  a

  ＜1”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：1112引用：68難度：0.8

  解析

• 3．函數

  f

  （

  x

  ）

  =

  1

  2

  x

  2

  -

  xsinx

  的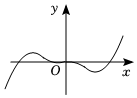大致圖象可能是（　　）

  A．	B．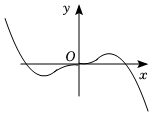
  C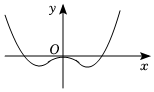．	D．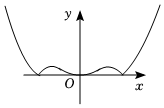
  組卷：255引用：9難度：0.8

  解析

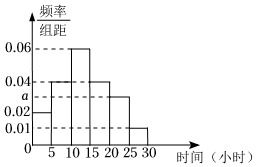• 4．某學校隨機抽取了部分學生，對他們每周使用手機的時間進行統計，得到如下的頻率分布直方圖．
  則下列說法：
  ①a=0.03；
  ②若抽取100人，則平均用時13.75小時；
  ③若從每周使用時間在[15，20），[20，25），[25，30）三組內的學生中用分層抽樣的方法選取8人進行訪談，則應從使用時間在[20，25）內的學生中選取的人數為3．
  其中正確的序號是（　　）

  A．①②

  B．①③

  C．②③

  D．①②③
  組卷：389引用：3難度：0.7

  解析

• 5．已知5^a=2，b=log₇3，c=

  1

  2

  log₅9，則a,b,c的大小關系為（　　）

  A．a＜b＜c

  B．a＜c＜b

  C．b＜a＜c

  D．c＜b＜a
  組卷：380引用：3難度：0.6

  解析

• 6．《九章算術》是我國古代的數學名著，其中有很多對幾何體體積的研究，已知某囤積糧食的容器的下面是一個底面積為32π，高為h的圓柱，上面是一個底面積為32π，高為h的圓錐，若該容器有外接球，則外接球的體積為（　　）

  A．36π

  B． 64 2 3 π

  C．288π

  D． 256 3 π
  組卷：531引用：4難度：0.5

  解析

三、解答題。（本大題共5小題，共75分）

• 19．已知數列{a_n}的前n項和

  A

  n

  =

  n

  2

  （

  n

  ∈

  N

  *

  ）

  ，

  b

  n

  =

  a

  n

  a

  n

  +

  1

  +

  a

  n

  +

  1

  a

  n

  （

  n

  ∈

  N

  *

  ）

  ，數列{b_n}的前n項和為B_n．
  （1）求數列{a_n}的通項公式；
  （2）設

  c

  n

  =

  a

  n

  2

  n

  （

  n

  ∈

  N

  *

  ）

  ，求數列{c_n}的前n項和C_n；
  （3）證明：

  2

  n

  ＜

  B

  n

  ＜

  2

  n

  +

  2

  （

  n

  ∈

  N

  *

  ）

  ．
  組卷：804引用：6難度：0.1

  解析

• 20．已知函數f（x）=ax^alnx（a＞0），g（x）=xe^x．
  （1）當a=1時，求曲線y=f（x）在x=e處的切線方程；
  （2）證明：g（x）≥lnx+x+1；
  （3）若f（x）≤g（x）對于任意的x＞1都成立，求a的最大值．
  組卷：448引用：2難度：0.5

  解析