2022-2023學(xué)年福建省泉州市鯉城區(qū)培元中學(xué)高一（上）期中數(shù)學(xué)試卷

一、選擇題：本大題共8小題，每小題5分，在每一個(gè)小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．設(shè)集合A={x|-2≤x≤3}，

  B

  =

  {

  x

  |

  x

  -

  1

  x

  -

  5

  ≤

  0

  }

  ，則A∪B=（　　）

  A．{x|-2≤x＜5}

  B．{x|1≤x≤3}

  C．{x|1≤x＜3}

  D．{x|-2≤x≤5}
  組卷：75引用：3難度：0.7

  解析

• 2．命題“

  ?

  a

  ∈

  R

  ，

  x

  -

  ax

  =

  0

  有實(shí)數(shù)解”的否定是（　　）

  A． ? a ∈ R ， x - ax = 0 無實(shí)數(shù)解	B． ? a ∈ R ， x - ax ≠ 0 有實(shí)數(shù)解
  C． ? a ∈ R ， x - ax ≠ 0 有實(shí)數(shù)解	D． ? a ∈ R ， x - ax = 0 無實(shí)數(shù)解
  組卷：108引用：8難度：0.9

  解析

• 3．已知

  f

  （

  x

  ）

  =

  x 2 ， x ＞ 0

  f （ x + 1 ） ， x ≤ 0

  ，則f（2）+f（-2）的值為（　　）

  A．6

  B．5

  C．4

  D．2
  組卷：111引用：19難度：0.9

  解析

• 4．設(shè)M={x|0≤x≤4}，N={y|-4≤y≤0}，函數(shù)f（x）的定義域?yàn)镸，值域?yàn)镹，則f（x）的圖象可以是（　　）

  A．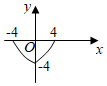

  B．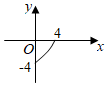

  C．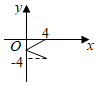

  D．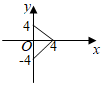
  組卷：357引用：8難度：0.9

  解析

• 5．已知函數(shù)f（x）=（m²-2m-2）?x^m-2是冪函數(shù)，且在（0，+∞）上遞增，則實(shí)數(shù)m=（　　）

  A．-1

  B．-1或3

  C．3

  D．2
  組卷：933引用：9難度：0.7

  解析

• 6．設(shè)正實(shí)數(shù)x,y滿足2x+y=1，則（　　）

  A．xy的最大值是 1 4	B． 2 x + 1 y 的最小值為9
  C．4x2+y2最小值為 1 2	D． 2 x + y 最大值為2
  組卷：393引用：13難度：0.6

  解析

• 7．若函數(shù)f（x）=x²-2ax+1-a在[0，2]上的最小值為-1．則a=（　　）

  A．1或2

  B．1

  C．1或 6 5

  D．-2
  組卷：431引用：5難度：0.7

  解析

三、解答題：本大題共6小題，解答應(yīng)寫出文字說明、證明過程或演算步驟。

• 21．隨著城市居民汽車使用率的增加，交通擁堵問題日益嚴(yán)重，而建設(shè)高架道路、地下隧道以及城市軌道公共運(yùn)輸系統(tǒng)等是解決交通擁堵問題的有效措施．某市城市規(guī)劃部門為提高早晚高峰期間某條地下隧道的車輛通行能力，研究了該隧道內(nèi)的車流速度v（單位：千米/小時(shí)）和車流密度x（單位：輛/千米）所滿足的關(guān)系式：

  v

  =

  60 ， 0 ＜ x ≤ 30

  80 - k 150 - x ， 30 ＜ x ≤ 120

  （

  k

  ∈

  R

  ）

  ．研究表明：當(dāng)隧道內(nèi)的車流密度達(dá)到120輛/千米時(shí)造成堵塞，此時(shí)車流速度是0千米/小時(shí)．
  （1）若車流速度v不小于40千米/小時(shí)，求車流密度x的取值范圍；
  （2）隧道內(nèi)的車流量y（單位時(shí)間內(nèi)通過隧道的車輛數(shù)，單位：輛/小時(shí)）滿足y=x?v,求隧道內(nèi)車流量的最大值（精確到1輛/小時(shí)），并指出當(dāng)車流量最大時(shí)的車流密度（精確到1輛/千米）．（參考數(shù)據(jù)：

  5

  ≈

  2

  .

  236

  ）
  組卷：230引用：14難度：0.4

  解析

• 22．已知定義在R上的函數(shù)f（x）滿足對(duì)任意的實(shí)數(shù)x,y均有f（xy）=f（x）f（y），且f（-1）=-1，當(dāng)0＜x＜1時(shí)，f（x）∈（0，1）．
  （1）判斷f（x）的奇偶性；
  （2）判斷f（x）在（0，+∞）上的單調(diào)性，并證明；
  （3）若對(duì)任意x₁，x₂∈[-1，1]，a∈[-1，1]，總有2|f（x₁）-f（x₂）|≤m²-2am+1恒成立，求實(shí)數(shù)m的取值范圍．
  組卷：277引用：6難度：0.4

  解析