2021-2022學(xué)年廣東省惠州一中八年級(jí)（下）期中數(shù)學(xué)試卷

一、選擇題。（本大題10小題，每小題3分，共30分．請(qǐng)將下列各題的答案涂在答題卡相應(yīng)的位置上）

• 1．下面各組數(shù)中，是勾股數(shù)的是（　　）

  A．9，16，25	B．0.3，0.4，0.5
  C．1，3，2	D．7，24，25
  組卷：333引用：8難度：0.6

  解析

• 2．如圖，直線a∥b,則直線a,b之間的距離是（　　）

  A．線段AB的長(zhǎng)度	B．線段CD的長(zhǎng)度
  C．線段AB	D．線段CD
  組卷：179引用：4難度：0.9

  解析

• 3．對(duì)于圓的面積公式S=πR²，下列說法中，正確的為（　　）

  A．π是自變量	B．R是常量
  C．R是自變量	D．π和R都是常量
  組卷：187引用：7難度：0.9

  解析

• 4．已知：

  20

  n

  是整數(shù)，則滿足條件的最小正整數(shù)n為（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：2022引用：58難度：0.9

  解析

• 5．下列各圖y是x的函數(shù)的是（　　）

  A．

  B．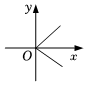

  C．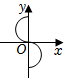

  D．
  組卷：711引用：9難度：0.7

  解析

• 6．在四邊形ABCD中，E，F(xiàn)，G，H分別為各邊的中點(diǎn)，順次連結(jié)E，F(xiàn)，G，H，得到中點(diǎn)四邊形EFGH．當(dāng)AC=BD時(shí)，則四邊形EFGH是（　　）

  A．平行四邊形

  B．矩形

  C．菱形

  D．正方形
  組卷：138引用：3難度：0.6

  解析

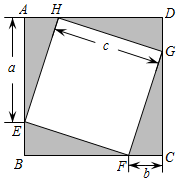• 7．如圖，將正方形ABCD剪去4個(gè)全等的直角三角形（圖中陰影部分），得到邊長(zhǎng)為c的四邊形EFGH．下列等式成立的是（　　）

  A．a(chǎn)+b=c	B．c2=（a+b）2-4ab
  C．c2=（a+b）（a-b）	D．a(chǎn)2+b2=c2
  組卷：285引用：3難度：0.6

  解析

• 8．如圖，在Rt△ABC中，∠ACB=90°，∠A=30°，AB=4，CD⊥AB于點(diǎn)D，E是AB的中點(diǎn)，則DE的長(zhǎng)為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：2863引用：18難度：0.8

  解析

五、解答題。（本大題2小題，每小題10分，共20分。請(qǐng)將各題的詳細(xì)答案寫在答題卡相應(yīng)的位置上）

• 24．【直觀想象】如圖1，動(dòng)點(diǎn)P在數(shù)軸上從負(fù)半軸向正半軸運(yùn)動(dòng)，點(diǎn)P到原點(diǎn)的距離先變小再變大，當(dāng)點(diǎn)P的位置確定時(shí)，點(diǎn)P到原點(diǎn)的距離也唯一確定；
  【數(shù)學(xué)發(fā)現(xiàn)】當(dāng)一個(gè)動(dòng)點(diǎn)P（x,0）到一個(gè)定點(diǎn)的距離為d,我們發(fā)現(xiàn)d是x的函數(shù)；
  【數(shù)學(xué)理解】（1）動(dòng)點(diǎn)P（x,0）到定點(diǎn)A（2，0）的距離為d,當(dāng)x=

  時(shí)，d取最小值；
  【類比遷移】（2）設(shè)動(dòng)點(diǎn)P（x,0）到兩個(gè)定點(diǎn)M（1，0）、N（3，0）的距離和為y.
  ①隨著x增大，y怎樣變化？
  ②在給出的平面直角坐標(biāo)系中畫出y關(guān)于x的函數(shù)圖象；
  ③當(dāng)y＞6時(shí)，x的取值范圍是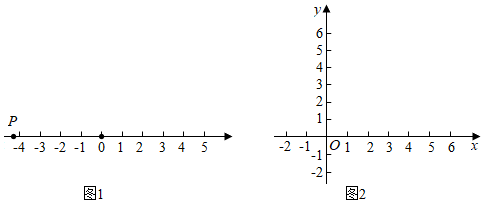

  ．
  
  組卷：1134引用：5難度：0.4

  解析

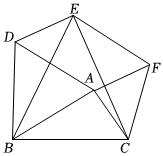• 25．（1）感知：如圖，分別以△ABC的三邊為邊長(zhǎng)，在BC邊的同側(cè)分別作三個(gè)等邊三角形，即△ABD，△BCE，△ACF，連接DE、EF，試猜想四邊形ADEF的形狀，并證明你的猜想．
  （2）應(yīng)用：當(dāng)△ABC中有AB=AC時(shí)，四邊形ADEF的形狀是

  ．
  （3）探究：①四邊形ADEF是否隨著△ABC形狀的改變而永遠(yuǎn)存在，簡(jiǎn)要說明理由；
  ②如果四邊形ADEF是正方形，則△ABC應(yīng)滿足什么條件？
  （4）若AB=4，AC=3，BC=5，求四邊形AFED的面積．
  組卷：66引用：2難度：0.3

  解析