當前位置：試卷中心 > 試卷詳情

2022-2023學年福建省福州市鼓樓區屏東中學高二（上）期末數學試卷

發布：2024/4/20 14:35:0

一、單項選擇題（本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

1．已知等比數列{a_n}中，a₂a₃a₄=27，a₆=24，則公比q=（　　）
A．-2 B．2 C．3 D．2或-2
組卷：267引用：7難度：0.9
解析
2．如果直線ax+2y+2=0與直線3x-y-2=0互相垂直，那么實數a=（　　）
A．
2
3
B．
-
2
3
C．
3
2
D．6
組卷：222引用：3難度：0.9
解析
3．已知拋物線x²=my焦點的坐標為F（0，1），P為拋物線上的任意一點，B（2，2），則|PB|+|PF|的最小值為（　　）
A．3 B．4 C．5 D．
11
2
組卷：191引用：6難度：0.6
解析
4．若等差數列的首項是-24，且從第10項開始大于0，則公差d的取值范圍是（　　）
A．
[
8
3
，
+
∞
）
B．（-∞，3） C．
[
8
3
，
3
）
D．
（
8
3
，
3
]
組卷：205引用：5難度：0.6
解析
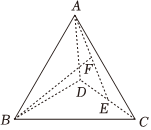5．在正四面體ABCD中，E是CD的中點，F是AE的中點，若
AB
=
a
，
AC
=
b
，
AD
=
c
，則
BF
=（　　）
A．
1
2
a
-
b
+
1
2
c
B．
a
+
1
4
b
-
1
4
c
C．
-
a
+
1
4
b
+
1
4
c
D．
1
4
a
-
b
+
1
4
c
組卷：234引用：3難度：0.9
解析
6．已知F₁，F₂是雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦點，點M是過坐標原點O且傾斜角為60°的直線l與雙曲線C的一個交點，且
|
M
F
1
+
M
F
2
|
=
|
M
F
1
-
M
F
2
|
則雙曲線C的離心率為（　　）
A．2 B．
2
+
3
C．
3
+
1
D．
3
組卷：172引用：7難度：0.6
解析
7．圖①是程陽永濟橋又名“風雨橋”，因為行人過往能夠躲避風雨而得名．已知程陽永濟橋上的塔從上往下看，其邊界構成的曲線可以看作正六邊形結構，如圖②所示，且各層的六邊形的邊長均為整數，從內往外依次成等差數列，若這四層六邊形的周長之和為156，且圖②中陰影部分的面積為
33
2
3
，則最外層六邊形的周長為（　　）
A．30 B．42 C．48 D．54
組卷：176引用：4難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本題共6小題，第17題10分，第18-22題每題12分，共70分，解答應寫出文字說明、證明過程或演算步驟，寫到答題卡對應題號的框格內．）

21．若橢圓
E
：
x
2
a
2
+
y
2
b
2
=
1
，
（
a
＞
b
＞
0
）
過拋物線x²=4y的焦點，且與雙曲線x²-y²=1有相同的焦點．
（1）求橢圓E的方程；
（2）不過原點O的直線l：y=x+m與橢圓E交于A、B兩點，求△ABO面積的最大值以及此時直線l的方程．
組卷：114引用：11難度：0.5
解析
22．設以△ABC的邊AB為長軸且過點C的橢圓Γ的方程為
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
橢圓Γ的離心率e=
1
2
，△ABC面積的最大值為
2
3
，AC和BC所在的直線分別與直線l：x=4相交于點M，N．
（1）求橢圓Γ的方程；
（2）設△ABC與△CMN的外接圓的面積分別為S₁，S₂，求
S
2
S
1
的最小值．
組卷：149引用：3難度：0.6
解析