人教新版九年級上冊《22.3 實際問題與二次函數（幾何圖形問題）》2023年同步練習卷

一、選擇題

• 1．矩形的周長為12cm,設其一邊長為x cm,面積為y cm²，則y與x的函數關系式及其自變量x的取值范圍均正確的是（　　）

  A．y=-x2+6x（3＜x＜6）	B．y=-x2+6x（0＜x＜6）
  C．y=-x2+12x（6＜x＜12）	D．y=-x2+12x（0＜x＜12）
  組卷：1408引用：6難度：0.6

  解析

• 2．在一個邊長為1的正方形中挖去一個邊長為x（0＜x＜1）的小正方形，如果設剩余部分的面積為y,那么y關于x的函數表達式為（　　）

  A．y=x2

  B．y=1-x2

  C．y=x2-1

  D．y=1-2x
  組卷：451引用：4難度：0.7

  解析

• 3．用一條長為60cm的繩子圍成一個面積為a cm²的長方形，a的值不可能為（　　）

  A．240

  B．225

  C．60

  D．30
  組卷：185引用：4難度：0.7

  解析

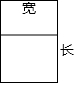• 4．用長度為8m的鋁合金條制成如圖所示的矩形窗框，那么這個窗戶的最大透光面積為（　　）m²．

  A． 25 6

  B． 8 3

  C．2

  D．4
  組卷：648引用：5難度：0.9

  解析

三、解答題

• 12．在一張足夠大的紙板上截取一個面積為3600平方厘米的矩形紙板ABCD，如圖1，再在矩形紙板的四個角上切去邊長相等的小正方形，再把它的邊沿虛線折起，做成一個無蓋的長方體紙盒，底面為矩形EFGH，如圖2．設小正方形的邊長為x厘米．
  （1）當矩形紙板ABCD的一邊長為90厘米時，求紙盒的側面積的最大值；
  （2）當EH：EF=7：2，且側面積與底面積之比為9：7時，求x的值．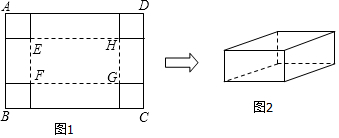
  
  組卷：345引用：2難度：0.1

  解析

• 13．某植物園有一塊足夠大的空地，其中有一堵長為6米的墻，現準備用20米的籬笆圍兩間矩形花圃，中間用籬笆隔開．小俊設計了如圖所示的兩種方案：
  
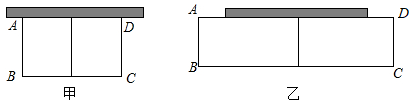
  方案甲中AD的長不超過墻長；方案乙中AD的長大于墻長．
  （1）若按方案甲施工，且圍成面積為25平方米的花圃，則AD的長是多少米？
  （2）按哪種方案施工，可以圍成的矩形花圃的面積最大？最大面積是多少？
  組卷：272引用：4難度：0.4

  解析