2022-2023學年江蘇省淮安市洪澤湖高級中學高二（下）第一次月考數學試卷

一、單項選擇題：（本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題意要求的.）

• 1．已知向量

  a

  =（8，-2，1），

  b

  =（-4，1，k），且

  a

  ∥

  b

  ，那么實數k的值為（　　）

  A． 1 2

  B． - 1 2

  C．-2

  D．2
  組卷：598引用：7難度：0.7

  解析

• 2．已知向量

  a

  =（1，1，0），

  b

  =（-1，0，2），且k

  a

  +

  b

  與2

  a

  +

  b

  互相垂直，則k的值是（　　）

  A．-1

  B． 4 3

  C． 5 3

  D． 7 5
  組卷：163引用：4難度：0.8

  解析

• 3．已知向量

  a

  =

  （

  -

  2

  ，

  1

  ，

  3

  ）

  ，

  b

  =

  （

  -

  1

  ，

  3

  ，

  2

  ）

  ，

  c

  =

  （

  1

  ，

  t

  ,-

  1

  ）

  共面，則實數t的值是（　　）

  A．1

  B．-1

  C．2

  D．-2
  組卷：425引用：6難度：0.7

  解析

• 4．若O、A、B、C為空間四點，且向量

  OA

  ，

  OB

  ，

  OC

  不能構成空間的一個基底，則（　　）

  A． OA ， OB ， OC 共線	B． OA ， OB 共線
  C． OB ， OC 共線	D．O，A，B，C四點共面
  組卷：1105引用：12難度：0.9

  解析

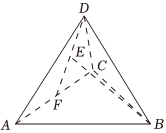• 5．在正四面體ABCD中，F是AC的中點，E是DF的中點，若

  DA

  =

  a

  ，

  DB

  =

  b

  ，

  DC

  =

  c

  ，則

  BE

  =（　　）

  A． 1 4 a - b + 1 4 c

  B． 1 2 a - b + 1 2 c

  C． 1 4 a + b + 1 4 c

  D． 1 2 a - b + c
  組卷：821引用：7難度：0.7

  解析

• 6．如圖，在平行六面體ABCD-A₁B₁C₁D₁中，若

  B

  D

  1

  =

  x

  C

  1

  D

  1

  +

  y

  C

  1

  B

  1

  +

  z

  C

  1

  C

  ，則有序實數組（x,y,z）為（　　）

  A．（1，1，1）

  B．（1，-1，-1）

  C．（1，1，-1）

  D．（-1，1，-1）
  組卷：165引用：4難度：0.7

  解析

• 7．若

  a

  =（1，λ，-1），

  b

  =（2，-1，2），且

  a

  與

  b

  的夾角的余弦為

  1

  9

  ，則|

  a

  |=（　　）

  A． 9 4

  B． 10 2

  C． 3 2

  D． 6
  組卷：894引用：3難度：0.9

  解析

四、解答題：（本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.）

• 21．如圖，在直三棱柱ABC-A₁B₁C₁中，AA₁=AB=2，∠ABC=90°．
  （1）求證：平面A₁BC⊥平面ABB₁A₁；
  （2）若AC與平面A₁BC所成的角為

  π

  6

  ，點E為線段A₁C的中點，求平面AEB與平面CEB夾角的大小．
  組卷：119引用：3難度：0.4

  解析

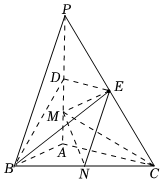• 22．如圖，在三棱錐P-ABC中，PA⊥底面ABC，∠BAC=90°，點D，E，N分別為棱PA，PC，BC的中點，M是線段AD的中點，PA=AC=4，AB=2．
  （Ⅰ）求證：MN∥平面BDE；
  （Ⅱ）求平面CEM與平面EMN的夾角的余弦值；
  （Ⅲ）已知點H在棱PA上，且直線NH與直線BE所成角的余弦值為

  7

  7

  ，求線段AH的長．
  組卷：411引用：7難度：0.5

  解析