2022-2023學(xué)年廣西貴港市高三（上）月考數(shù)學(xué)試卷（文科）（12月份）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．已知復(fù)數(shù)z滿(mǎn)足（z+1）（2-i）=5，則

  z

  =（　　）

  A．1+i

  B．3-i

  C．3+i

  D．1-i
  組卷：11引用：2難度：0.7

  解析

• 2．設(shè)集合A={-1，0，1，2}，B={x|x²-4＜0}，則A∩B=（　　）

  A．{-1，0，1，2}

  B．{0，1，2}

  C．{-1，0，1}

  D．{-1，0，2}
  組卷：13引用：2難度：0.8

  解析

• 3．如圖是某統(tǒng)計(jì)部門(mén)網(wǎng)站發(fā)布的《某市2020年2～12月國(guó)民經(jīng)濟(jì)和社會(huì)發(fā)展統(tǒng)計(jì)公報(bào)》中居民消費(fèi)價(jià)格指數(shù)（CPI）月度漲跌幅度折線(xiàn)圖（注：同比是今年第n個(gè)月與去年第n個(gè)月相比，環(huán)比是現(xiàn)在的統(tǒng)計(jì)周期和上一個(gè)統(tǒng)計(jì)周期相比）
  
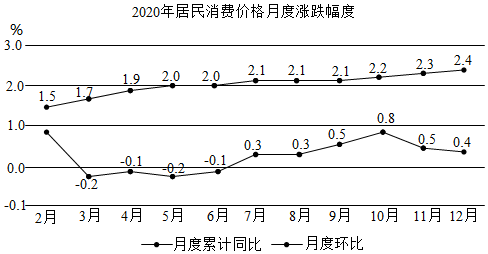
  下列說(shuō)法錯(cuò)誤的是（　　）
  ①2020年9月CPI環(huán)比上升0.5%，同比上漲2.1%
  ②2020年9月CP1環(huán)比上升0.2%，同比無(wú)變化
  ③2020年3月CPI環(huán)比下降1.1%，同比上漲0.2%
  ④2020年3月CPI環(huán)比下降0.2%，同比上漲1.7%

  A．①③

  B．①④

  C．②④

  D．②③
  組卷：201引用：7難度：0.9

  解析

• 4．“l(fā)ga＞lgb”是“（a-2）³＞（b-2）³”的（　　）

  A．充要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：8引用：2難度：0.8

  解析

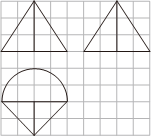• 5．公元5世紀(jì)，我國(guó)古代著名數(shù)學(xué)家祖沖之給出了圓周率π的兩個(gè)近似分?jǐn)?shù)值：

  22

  7

  （稱(chēng)為“約率”）和

  355

  113

  （稱(chēng)為“密率”）．一幾何體的三視圖如圖所示（每個(gè)小方格的邊長(zhǎng)為1），如果取圓周率為“密率”，則該幾何體的體積為（　　）

  A． 1160 113

  B． 1161 113

  C． 1162 113

  D． 1163 113
  組卷：27引用：2難度：0.5

  解析

• 6．函數(shù)f（x）=sinxln

  π

  -

  x

  π

  +

  x

  在（-π，π）的圖象大致為（　　）

  A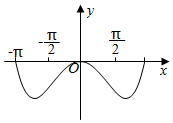．	B．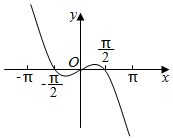
  C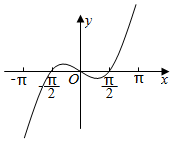．	D．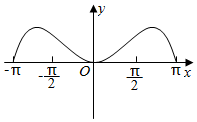
  組卷：178引用：4難度：0.8

  解析

• 7．若函數(shù)f（x）=（x²-ax-2）e^x有極值點(diǎn)為0，則f′（2）=（　　）

  A．14e2

  B．12e2

  C． 14 e 2

  D． 12 e 2
  組卷：35引用：1難度：0.7

  解析

（二）選考題：共10分.請(qǐng)考生在22、23題中任選一題作答，如果多做，則按所做的第一題計(jì)分.[選修4一4；坐標(biāo)系與參數(shù)方程]

• 22．在平面直角坐標(biāo)系xOy中，直線(xiàn)l₁的參數(shù)方程為

  x = t - 3

  y = kt

  （t為參數(shù)），直線(xiàn)l₂的參數(shù)方程為

  x = 3 - m

  y = m 3 k

  （m為參數(shù)），設(shè)直線(xiàn)l₁與l₂的交點(diǎn)為P，當(dāng)k變化時(shí)點(diǎn)P的軌跡為曲線(xiàn)C₁．
  （1）求曲線(xiàn)C₁的普通方程；
  （2）以坐標(biāo)原點(diǎn)為極點(diǎn)，x軸的非負(fù)半軸為極軸建立極坐標(biāo)系，直線(xiàn)C₂的極坐標(biāo)方程為

  ρsin

  （

  θ

  +

  π

  4

  ）

  =

  3

  2

  ，點(diǎn)Q為曲線(xiàn)C₁上的動(dòng)點(diǎn)，求點(diǎn)Q到直線(xiàn)C₂的距離的最大值．
  組卷：58引用：2難度：0.7

  解析

[選修4一5；不等式選講]

• 23．已知a,b,c∈R⁺．
  （1）證明：

  a

  2

  +

  b

  2

  +

  c

  2

  ≥

  a

  +

  2

  b

  +

  2

  c

  3

  ；
  （2）若a²+2b²=9，求a+4b的最大值．
  組卷：16引用：2難度：0.5

  解析