2013-2014學年四川省成都七中高三（下）周練數學試卷（文科）

一、選擇題（每小題5分，共50分）

• 1．若復數z滿足：z+|z|=1+2i,則z的虛部為（　　）

  A．2i

  B．1

  C．2

  D．i
  組卷：103引用：9難度：0.9

  解析

• 2．設全集U是實數集R，M={x||2x-3|≥4x}，N={x|

  log

  1

  3

  （x+2）≥0}，則M∩N=（　　）

  A．{x|x≤- 1 2 }

  B．{x|x≤-1}

  C．{x|-1≤x≤- 1 2 }

  D．{x|-2＜x≤-1}
  組卷：10引用：3難度：0.9

  解析

• 3．設a∈R，則“a=-2”是“直線l₁：ax+2y-1=0與直線l₂：x+（a+1）y+2=0平行”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：137引用：4難度：0.9

  解析

• 4．閱讀如圖所示的程序框圖，運行相應的程序，輸出的結果k=（　　）
  

  A．4

  B．5

  C．6

  D．7
  組卷：18引用：6難度：0.9

  解析

• 5．設a、b是兩條不同的直線，α、β是兩個不同的平面，下列命題中正確的是（　　）

  A．若a∥b,a∥α，則b∥α	B．若α⊥β，a∥α，則a⊥β
  C．若α⊥β，a⊥β，則a∥α	D．若a⊥b,a⊥α，b⊥β，則α⊥β
  組卷：435引用：46難度：0.7

  解析

• 6．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的一條漸近線與圓（x-3）²+y²=8相交于A，B兩點，且|AB|=4，則此雙曲線的離心率為（　　）

  A．5

  B． 5 3 3

  C． 3 5 5

  D． 5
  組卷：217引用：12難度：0.9

  解析

• 7．一個空間幾何體的三視圖如圖所示，則該幾何體的表面積為（　　）
  

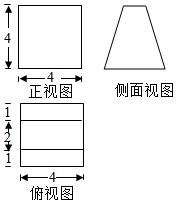
  A．48

  B．32+8 17

  C．48+8 17

  D．80
  組卷：701引用：47難度：0.9

  解析

三、解答題（共75分）

• 20．已知函數f（x）=lnx+ax+1（a∈R）．
  （Ⅰ）若a=1時，求曲線y=f（x）在點（1，f（1））處的切線方程；
  （Ⅱ）求f（x）的單調區間；
  （Ⅲ）設g（x）=2^x-1，若存在x₁∈（0，+∞），對于任意x₂∈[0，1]，使f（x₁）≥g（x₂），求a的取值范圍．
  組卷：73引用：9難度：0.3

  解析

• 21．已知橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞c＞0）的左右焦點分別為F₁，F₂，c為半焦距，若以F₂為圓心，b-c為半徑作圓F₂，過橢圓上一點P作此圓的切線，切點為T，且|PT|的最小值不小于

  3

  2

  （a-c），
  （1）求橢圓離心率的取值范圍；
  （2）設橢圓的短半軸長為1，圓F₂與x軸的右交點為Q，過點Q作斜率為k（k＞0）的直線l與橢圓相交于A，B兩點，與圓F₂交于C，D兩點，若O在以AB為直徑的圓上，求|

  CD

  |的最大值．
  組卷：78引用：3難度：0.1

  解析