2022-2023學年河南省駐馬店市開發區高級中學高二(上)期中數學試卷
發布:2024/11/5 19:0:9
一、選擇題(共12小題,每小題5分,共60分)
-
1.已知a,b為實數,直線l1:ax+2y-1=0與直線l2:(a+1)x-2ay+1=0垂直,則a=( )
A.0或3 B.3 C.0 D.無解 組卷:154引用:2難度:0.7 -
2.若直線l的方向向量為
,平面α的法向量為m,則能使l∥α的是( )nA. =(1,2,1),m=(1,0,1)nB. =(0,1,0),m=(0,3,0)nC. =(1,-2,3),m=(-2,2,2)nD. =(0,2,1),m=(-1,0,-1)n組卷:488引用:6難度:0.7 -
3.若向量
=(1,λ,0),a=(2,-1,2),且b與a的夾角余弦值為b,則實數λ等于( )23A.0 B.- 43C.0或- 43D.0或 43組卷:994引用:13難度:0.9 -
4.已知雙曲線
-x2a2=1的左、右焦點分別為F1,F2,O為坐標原點,|F1F2|=10.點M是雙曲線左支上的一點,若|OM|=y2b2,4|MF1|=3|MF2|,則雙曲線的標準方程是( )a2+b2A. x24-y221=1B. x221-y24=1C. x2-y224=1D. =1x224-y2組卷:158引用:2難度:0.6 -
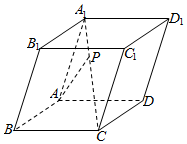 5.如圖,在平行六面體ABCD-A1B1C1D1中,=AA1,a=AB,b=AD,點P在c上,且A1P:PC=2:3,則A1C等于( )AP
5.如圖,在平行六面體ABCD-A1B1C1D1中,=AA1,a=AB,b=AD,點P在c上,且A1P:PC=2:3,則A1C等于( )APA. 25+a35+b35cB. 35+a25+b25cC.- 25+a25+b35cD. 35-a25-b25c組卷:176引用:5難度:0.7 -
6.已知{
,a,b}為空間的一組基底,則下列向量也能作為空間的一組基底的是( )cA. +a,b+b,c-acB. +2a,b,b+acC.2 +a,b+2b,c+a+bcD. +a,c+2b,a-2bc組卷:102引用:6難度:0.8 -
7.已知拋物線的焦點在直線x-2y-4=0上,則此拋物線的標準方程是( )
A.y2=16x B.x2=-8y C.y2=16x或x2=-8y D.y2=16x或x2=8y 組卷:247引用:10難度:0.9
三、解答題(共6小題,共70分)
-
 21.如圖,PO是三棱錐P-ABC的高,PA=PB,AB⊥AC,E為PB的中點.
21.如圖,PO是三棱錐P-ABC的高,PA=PB,AB⊥AC,E為PB的中點.
(1)證明:OE∥平面PAC;
(2)若∠ABO=∠CBO=30°,PO=3,PA=5,求二面角C-AE-B的正弦值.組卷:7936引用:11難度:0.5 -
22.已知橢圓C:
的右焦點為F(1,0),離心率x2a2+y2b2=1.e=33
(1)求橢圓C的標準方程;
(2)已知動直線l過點F,且與橢圓C交于A,B兩點,試問x軸上是否存在定點M,使得恒成立?若存在,求出點M的坐標,若不存在,請說明理由.MA?MB=-119組卷:76引用:4難度:0.5


