當前位置：試卷中心 > 試卷詳情

2022-2023學年北京市海淀區育英中學高三（上）統測數學試卷（二）

發布：2024/7/21 8:0:9

一、選擇題：本大題共10小題，每小題4分，共40分。在每小題列出的四個選項中，選出符合題目要求的一項。

1．已知集合A={x|x²+5x-6＜0}，B={x|x＞-2}，則A∩B=（　　）
A．（-2，+∞） B．（-6，-2） C．（-2，1） D．（-2，6）
組卷：488引用：5難度：0.8
解析
2．“sinx=
2
2
”是“
x
=
2
kπ
+
π
4
（
k
∈
Z
）
”的（　　）
A．必要不充分條件 B．充分不必要條件
C．充要條件 D．既不充分也不必要條件
組卷：81引用：4難度：0.8
解析
3．已知
sin
（
α
-
π
3
）
=
2
3
，則
cos
（
2
α
+
π
3
）
=（　　）
A．
-
1
9
B．
1
9
C．
-
4
5
9
D．
4
5
9
組卷：1045引用：8難度：0.8
解析
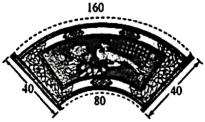4．玉雕壁畫是采用傳統的手工雕刻工藝，加工生產成的玉雕工藝畫．某扇形玉雕壁畫尺寸（單位：cm）如圖所示，則該玉雕壁畫的扇面面積約為（　　）
A．1600cm² B．3200cm² C．3350cm² D．4800cm²
組卷：140引用：4難度：0.6
解析
5．要得到
g
（
x
）
=
sin
（
4
x
+
2
π
3
）
的圖象，只需要將f（x）=cos²2x-sin²2x的圖象（　　）
A．向左平移
π
24
個單位長度
B．向右平移
π
24
個單位長度
C．向左平移
π
12
個單位長度
D．向右平移
π
12
個單位長度
組卷：129引用：5難度：0.7
解析
6．設函數f（x）=|sinx|，若a=f（ln2），
b
=
f
（
log
1
3
2
）
，
c
=
f
（
3
1
2
）
，則（　　）
A．a＜b＜c B．b＜c＜a C．c＜a＜b D．b＜a＜c
組卷：181引用：3難度：0.7
解析
7．中國的5G技術領先世界，5G技術極大地提高了數據傳輸速率，最大數據傳輸速率C取決于信道帶寬W，經科學研究表明：C與W滿足C=Wlog₂（1+T），其中T為信噪比．若不改變帶寬W，而將信噪比T從9提升到39，則C大約增加了（　　）（附：lg2≈0.3）
A．20% B．40% C．60% D．80%
組卷：87引用：7難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題：本大題共6小題，共85分。解答應寫出必要的文字說明、證明過程或演算步驟。

20．已知：函數f（x）=sinx-xcosx.
（1）求f（π）；
（2）求證：當x∈（0，
π
2
）時，f（x）＜
1
3
x³；
（3）若f（x）＞kx-xcosx對x∈（0，
π
2
）恒成立，求實數k的最大值．
組卷：221引用：4難度：0.3
解析
21．有限數列{a_n}，若滿足|a₁-a₂|≤|a₁-a₃|≤…≤|a₁-a_m|，m是項數p,則稱{a_n}滿足性質p.
（1）判斷數列3，2，5，1和4，3，2，5，1是否具有性質p,請說明理由；
（2）若a₁=1，公比為q的等比數列，項數為10，具有性質p,求q的取值范圍；
（3）若a_n是1，2，3，…，m的一個排列（m≥4），b_k=a_k+1（k=1，2，…，m-1），{a_n}，{b_n}都具有性質p,求所有滿足條件的{a_n}．
組卷：41引用：2難度：0.2
解析