滬教新版八年級（下）中考題單元試卷：第23章 概率初步（19）

一、選擇題（共3小題）

• 1．已知甲袋有5張分別標示1～5的號碼牌，乙袋有6張分別標示6～11的號碼牌，慧婷分別從甲、乙兩袋中各抽出一張號碼牌．若同一袋中每張號碼牌被抽出的機會相等，則她抽出兩張號碼牌，其數字乘積為3的倍數的幾率為何？（　　）

  A． 1 10

  B． 1 3

  C． 7 15

  D． 8 15
  組卷：109引用：59難度：0.9

  解析

• 2．同時拋擲A、B兩個均勻的小立方體（每個面上分別標有數字1，2，3，4，5，6），設兩立方體朝上的數字分別為x、y,并以此確定點P（x,y），那么點P落在拋物線y=-x²+3x上的概率為（　　）

  A． 1 18

  B． 1 12

  C． 1 9

  D． 1 6
  組卷：318引用：70難度：0.7

  解析

• 3．一個不透明的袋子里裝著質地、大小都相同的3個紅球和2個綠球，隨機從中摸出一球，不再放回袋中，充分攪勻后再隨機摸出一球．兩次都摸到紅球的概率是（　　）

  A． 3 10

  B． 9 25

  C． 9 20

  D． 3 5
  組卷：586引用：81難度：0.7

  解析

二、填空題（共3小題）

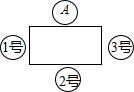• 4．合作小組的4位同學坐在課桌旁討論問題，學生A的座位如圖所示，學生B，C，D隨機坐到其他三個座位上，則學生B坐在2號座位的概率是

   

  ．
  組卷：477引用：83難度：0.7

  解析

• 5．在1，2，3，4四個數字中隨機選兩個不同的數字組成兩位數，則組成的兩位數大于40的概率是

   

  ．
  組卷：226引用：62難度：0.5

  解析

• 6．從-3、1、-2這三個數中任取兩個不同的數，積為正數的概率是

  ．
  組卷：156引用：63難度：0.7

  解析

三、解答題（共24小題）

• 7．一個不透明的口袋中裝有4張卡片，卡片上分別標有數字1、-2、-3、4，它們除了標有的數字不同之外再也沒有其它區別，小芳從盒子中隨機抽取一張卡片．
  （1）求小芳抽到負數的概率；
  （2）若小明再從剩余的三張卡片中隨機抽取一張，請你用樹狀圖或列表法，求小明和小芳兩人均抽到負數的概率．
  組卷：148引用：69難度：0.7

  解析

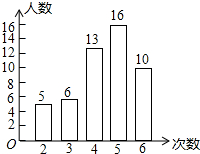• 8．（1）我市開展了“尋找雷鋒足跡”的活動，某中學為了了解七年級800名學生在“學雷鋒活動月”中做好事的情況，隨機調查了七年級50名學生在一個月內做好事的次數，并將所得數據繪制成統計圖，請根據圖中提供的信息解答下列問題：
  ①所調查的七年級50名學生在這個月內做好事次數的平均數是

   

  ，眾數是

   

  ，極差是

   

  ：
  ②根據樣本數據，估計該校七年級800名學生在“學雷鋒活動月”中做好事不少于4次的人數．
  （2）甲口袋有2個相同的小球，它們分別寫有數字1和2；乙口袋中裝有3個相同的小球，它們分別寫有數字3、4和5，從這兩個口袋中各隨機地取出1個小球．
  ①用“樹狀圖法”或“列表法”表示所有可能出現的結果；
  ②取出的兩個小球上所寫數字之和是偶數的概率是多少？
  組卷：197引用：63難度：0.5

  解析

• 9．小明與甲、乙兩人一起玩“手心手背”的游戲．他們約定：如果三人中僅有一人出“手心”或“手背”，則這個人獲勝；如果三人都出“手心”或“手背”，則不分勝負，那么在一個回合中，如果小明出“手心”，則他獲勝的概率是多少？（請用“畫樹狀圖”或“列表”等方法寫出分析過程）
  組卷：229引用：65難度：0.7

  解析

• 10．端午節吃粽子是中華民族的傳統習俗，據了解，甲廠家生產了A，B，C三個品種的盒裝粽子，乙廠家生產D，E兩個品種的盒裝粽子，端午節前，某商場在甲乙兩個廠家中各選購一個品種的盒裝粽子銷售．
  （1）試用樹狀圖或列表法寫出所有選購方案；
  （2）如果（1）中各種選購方案被選中的可能性相同，那么甲廠家的B品種粽子被選中的概率是多少？
  組卷：136引用：61難度：0.7

  解析

三、解答題（共24小題）

• 29．在不透明的袋子中有四張標著數字1，2，3，4的卡片，小明、小華兩人按照各自的規則玩抽卡片游戲．
  小明畫出樹狀圖如圖所示：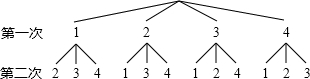
  
  小華列出表格如下：
  

  第一次 第二次	1	2	3	4
  1	（1，1）	（2，1）	（3，1）	（4，1）
  2	（1，2）	（2，2）	①	（4，2）
  3	（1，3）	（2，3）	（3，3）	（4，3）
  4	（1，4）	（2，4）	（3，4）	（4，4）

  回答下列問題：
  （1）根據小明畫出的樹形圖分析，他的游戲規則是，隨機抽出一張卡片后

  （填“放回”或“不放回”），再隨機抽出一張卡片；
  （2）根據小華的游戲規則，表格中①表示的有序數對為

  ；
  （3）規定兩次抽到的數字之和為奇數的獲勝，你認為誰獲勝的可能性大？為什么？
  組卷：347引用：63難度：0.5

  解析

• 30．一不透明的布袋里，裝有紅、黃、藍三種顏色的小球（除顏色外其余都相同），其中有紅球2個，藍球1個，黃球若干個，現從中任意摸出一個球是紅球的概率為

  1

  2

  ．
  （1）求口袋中黃球的個數；
  （2）甲同學先隨機摸出一個小球（不放回），再隨機摸出一個小球，請用“樹狀圖法”或“列表法”，求兩次摸出都是紅球的概率；
  （3）現規定：摸到紅球得5分，摸到黃球得3分，摸到藍球得2分（每次摸后放回），乙同學在一次摸球游戲中，第一次隨機摸到一個紅球第二次又隨機摸到一個藍球，若隨機再摸一次，求乙同學三次摸球所得分數之和不低于10分的概率．
  組卷：357引用：69難度：0.3

  解析