當前位置：試卷中心 > 試卷詳情

北師大版必修4高考題單元試卷：第2章平面向量（03）

發布：2024/12/26 22:0:2

一、選擇題（共13小題）

1．已知向量
m
=（λ+1，1），
n
=（λ+2，2），若（
m
+
n
）⊥（
m
-
n
），則λ=（　　）
A．-4 B．-3 C．-2 D．-1
組卷：8000引用：103難度：0.9
解析
2．已知
a
，
b
是單位向量，
a
?
b
=0．若向量
c
滿足|
c
-
a
-
b
|=1，則|
c
|的最大值為（　　）
A．
2
-
1
B．
2
C．
2
+
1
D．
2
+
2
組卷：1772引用：25難度：0.9
解析
3．若非零向量
a
，
b
滿足|
a
|=
2
2
3
|
b
|，且（
a
-
b
）⊥（3
a
+2
b
），則
a
與
b
的夾角為（　　）
A．
π
4
B．
π
2
C．
3
π
4
D．π
組卷：5655引用：69難度：0.9
解析
4．已知非零向量
a
，
b
滿足|
b
|=4|
a
|，且
a
⊥（
2
a
+
b
），則
a
與
b
的夾角為（　　）
A．
π
3
B．
π
2
C．
2
π
3
D．
5
π
6
組卷：7124引用：64難度：0.9
解析
5．設
a
=（1，2），
b
=（1，1），
c
=
a
+k
b
，若
b
⊥
c
，則實數k的值等于（　　）
A．-
3
2
B．-
5
3
C．
5
3
D．
3
2
組卷：4842引用：50難度：0.9
解析
6．已知向量
a
=
（
-
5
，
6
）
，
b
=
（
6
，
5
）
，則
a
與
b
（　　）
A．垂直 B．不垂直也不平行
C．平行且同向 D．平行且反向
組卷：823引用：35難度：0.9
解析
7．已知向量
a
=（1，0，-1），則下列向量中與
a
成60°夾角的是（　　）
A．（-1，1，0） B．（1，-1，0） C．（0，-1，1） D．（-1，0，1）
組卷：952引用：36難度：0.9
解析
8．已知向量
a
=（1，
3
），
b
=（3，m），若向量
a
，
b
的夾角為
π
6
，則實數m=（　　）
A．2
3
B．
3
C．0 D．-
3
組卷：2621引用：46難度：0.9
解析
9．平面向量
a
=（1，2），
b
=（4，2），
c
=m
a
+
b
（m∈R），且
c
與
a
的夾角等于
c
與
b
的夾角，則m=（　　）
A．-2 B．-1 C．1 D．2
組卷：2221引用：32難度：0.7
解析
10．設
a
，
b
為非零向量，|
b
|=2|
a
|，兩組向量
x
1
，
x
2
，
x
3
，
x
4
和
y
1
，
y
2
，
y
3
，
y
4
，均由2個
a
和2個
b
排列而成，若
x
1
?
y
1
+
x
2
?
y
2
+
x
3
?
y
3
+
x
4
?
y
4
所有可能取值中的最小值為4|
a
|²，則
a
與
b
的夾角為（　　）
A．
2
π
3
B．
π
3
C．
π
6
D．0
組卷：1050引用：30難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（共4小題）

29．設向量
a
=
（
3
sinx
,
sinx
）
，
b
=
（
cosx
,
sinx
）
，
x
∈
[
0
，
π
2
]
．
（1）若
|
a
|
=
|
b
|
，求x的值；
（2）設函數
f
（
x
）
=
a
?
b
，求f（x）的最大值．
組卷：2724引用：52難度：0.5
解析
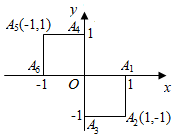30．小波以游戲方式決定是去打球、唱歌還是去下棋．游戲規則為以O為起點，再從A₁，A₂，A₃，A₄，A₅，A₆（如圖）這6個點中任取兩點分別為終點得到兩個向量，記這兩個向量的數量積為X，若X＞0就去打球，若X=0就去唱歌，若X＜0就去下棋．
（1）寫出數量積X的所有可能取值；
（2）分別求小波去下棋的概率和不去唱歌的概率．
組卷：531引用：36難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．垂直	B．不垂直也不平行
C．平行且同向	D．平行且反向

北師大版必修4高考題單元試卷：第2章 平面向量（03）

一、選擇題（共13小題）

1．已知向量m=（λ+1，1），n=（λ+2，2），若（m+n）⊥（m-n），則λ=（ ）

2．已知a，b是單位向量，a?b=0．若向量c滿足|c-a-b|=1，則|c|的最大值為（ ）

3．若非零向量a，b滿足|a|=223|b|，且（a-b）⊥（3a+2b），則a與b的夾角為（ ）

4．已知非零向量a，b滿足|b|=4|a|，且a⊥（2a+b），則a與b的夾角為（ ）

5．設a=（1，2），b=（1，1），c=a+kb，若b⊥c，則實數k的值等于（ ）

6．已知向量a=（-5，6），b=（6，5），則a與b（ ）

7．已知向量a=（1，0，-1），則下列向量中與a成60°夾角的是（ ）

8．已知向量a=（1，3），b=（3，m），若向量a，b的夾角為π6，則實數m=（ ）

9．平面向量a=（1，2），b=（4，2），c=ma+b（m∈R），且c與a的夾角等于c與b的夾角，則m=（ ）

10．設a，b為非零向量，|b|=2|a|，兩組向量x1，x2，x3，x4和y1，y2，y3，y4，均由2個a和2個b排列而成，若x1?y1+x2?y2+x3?y3+x4?y4所有可能取值中的最小值為4|a|2，則a與b的夾角為（ ）

三、解答題（共4小題）

29．設向量a=（3sinx,sinx），b=（cosx,sinx），x∈[0，π2]．（1）若|a|=|b|，求x的值；（2）設函數f（x）=a?b，求f（x）的最大值．

北師大版必修4高考題單元試卷：第2章平面向量（03）

1．已知向量
m
=（λ+1，1），
n
=（λ+2，2），若（
m
+
n
）⊥（
m
-
n
），則λ=（　　）

2．已知
a
，
b
是單位向量，
a
?
b
=0．若向量
c
滿足|
c
-
a
-
b
|=1，則|
c
|的最大值為（　　）

3．若非零向量
a
，
b
滿足|
a
|=
2
2
3
|
b
|，且（
a
-
b
）⊥（3
a
+2
b
），則
a
與
b
的夾角為（　　）

4．已知非零向量
a
，
b
滿足|
b
|=4|
a
|，且
a
⊥（
2
a
+
b
），則
a
與
b
的夾角為（　　）

5．設
a
=（1，2），
b
=（1，1），
c
=
a
+k
b
，若
b
⊥
c
，則實數k的值等于（　　）

6．已知向量
a
=
（
-
5
，
6
）
，
b
=
（
6
，
5
）
，則
a
與
b
（　　）

7．已知向量
a
=（1，0，-1），則下列向量中與
a
成60°夾角的是（　　）

8．已知向量
a
=（1，
3
），
b
=（3，m），若向量
a
，
b
的夾角為
π
6
，則實數m=（　　）

9．平面向量
a
=（1，2），
b
=（4，2），
c
=m
a
+
b
（m∈R），且
c
與
a
的夾角等于
c
與
b
的夾角，則m=（　　）

10．設
a
，
b
為非零向量，|
b
|=2|
a
|，兩組向量
x
1
，
x
2
，
x
3
，
x
4
和
y
1
，
y
2
，
y
3
，
y
4
，均由2個
a
和2個
b
排列而成，若
x
1
?
y
1
+
x
2
?
y
2
+
x
3
?
y
3
+
x
4
?
y
4
所有可能取值中的最小值為4|
a
|²，則
a
與
b
的夾角為（　　）

29．設向量
a
=
（
3
sinx
,
sinx
）
，
b
=
（
cosx
,
sinx
）
，
x
∈
[
0
，
π
2
]
．
（1）若
|
a
|
=
|
b
|
，求x的值；
（2）設函數
f
（
x
）
=
a
?
b
，求f（x）的最大值．