2022-2023學年浙江省七彩陽光新高考研究聯盟高一（下）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項符合題目要求的.

• 1．已知集合A={x|x²＜9}，B={x|-1＜x≤5}，則A∩B=（　　）

  A．{x|-3＜x＜3}

  B．{x|-1＜x＜5}

  C．{x|-1＜x＜3}

  D．{x|-3＜x≤5}
  組卷：69引用：2難度：0.8

  解析

• 2．若|z|=4，則

  z

  ?

  z

  =（　　）

  A．32

  B．16

  C．4

  D．2
  組卷：32引用：3難度：0.8

  解析

• 3．“A=30°”是“sinA=

  1

  2

  ”的（　　）條件．

  A．必要不充分	B．充分不必要
  C．充要	D．既不充分也不必要
  組卷：15引用：3難度：0.9

  解析

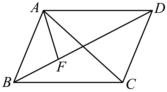• 4．如圖所示，F為平行四邊形ABCD對角線BD上一點，

  BF

  =

  1

  3

  FD

  ，則

  AF

  =（　　）

  A． 3 4 AB + 1 4 AD

  B． 3 4 AB - 1 4 AD

  C． 1 4 AB + 3 4 AD

  D． 1 4 AB - 3 4 AD
  組卷：204引用：4難度：0.9

  解析

• 5．已知

  sin

  （

  π

  3

  +

  α

  ）

  =

  2

  3

  ，則

  cos

  （

  7

  π

  6

  -

  α

  ）

  的值等于（　　）

  A． 2 3

  B． - 2 3

  C． 5 3

  D． ± 5 3
  組卷：474引用：3難度：0.7

  解析

• 6．已知向量

  a

  =

  （

  2

  ，

  1

  ）

  ，

  b

  =

  （

  -

  1

  ，

  1

  ）

  ，向量

  a

  在

  b

  方向上的投影向量為（　　）

  A． 2 2 b

  B． - 2 2 b

  C． 1 2 b

  D． - 1 2 b
  組卷：131引用：4難度：0.8

  解析

• 7．如圖扇形ABC，圓心角A=90°，D為半徑AB中點，CB，CD把扇形分成三部分，這三部分繞AC旋轉一周，所得三部分旋轉體的體積V₁，V₂，V₃之比是（　　）

  A．1：2：2

  B．1：2：3

  C．1：3：3

  D．1：3：4
  組卷：81引用：2難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟．

• 21．設△ABC的內角A，B，C的對邊分別為a,b,c,已知

  1

  -

  sin

  A

  cos

  A

  =

  1

  -

  cos

  2

  B

  sin

  2

  B

  ．
  （1）判斷△ABC的形狀（銳角、直角、鈍角三角形），并給出證明；
  （2）求

  4

  a

  2

  +

  5

  b

  2

  c

  2

  的最小值．
  組卷：111引用：2難度：0.5

  解析

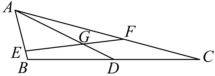• 22．如圖，△ABC中AB=1，AC=3，∠BAC=60°，AD為BC邊上的中線，點E，F分別為邊AB，AC上的動點，線段EF交AD于G，且線段AE與線段AF的長度乘積為1．
  （1）已知AF=2，請用

  AB

  ，

  AC

  表示

  AG

  ；
  （2）求

  AG

  ?

  EF

  的取值范圍．
  組卷：206引用：4難度：0.5

  解析