2022-2023學年福建省南平市建甌市芝華中學高三（上）暑期數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分

• 1．設集合A={-1，1，2，3，5，6}，B={2，3，4}，C={x∈R|1≤x＜3}，則（A∩C）∪B=（　　）

  A．{2}

  B．{2，3}

  C．{-1，2，3}

  D．{1，2，3，4}
  組卷：711引用：10難度：0.9

  解析

• 2．設純虛數z滿足

  1

  -

  i

  z

  =1+ai（其中i為虛數單位），則實數a等于（　　）

  A．1

  B．-1

  C．2

  D．-2
  組卷：100引用：2難度：0.8

  解析

• 3．已知a=

  2

  -

  1

  3

  ，b=log₂

  1

  3

  ，c=

  log

  1

  2

  1

  3

  ，則（　　）

  A．a＞b＞c

  B．a＞c＞b

  C．c＞b＞a

  D．c＞a＞b
  組卷：3320引用：65難度：0.9

  解析

• 4．函數f（x）=x^a滿足f（2）=4，那么函數g（x）=|log_a（x+1）|的圖象大致為（　　）

  A．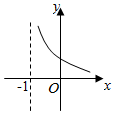

  B．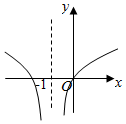

  C．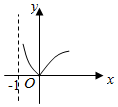

  D．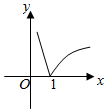
  組卷：640引用：47難度：0.7

  解析

• 5．若向量

  a

  ，

  b

  滿足

  a

  ?

  （

  a

  -

  b

  ）

  =5，|

  a

  |=2，|

  b

  |=1，則向量

  a

  ，

  b

  的夾角為（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  組卷：258引用：5難度：0.7

  解析

• 6．已知sin（π+θ）=-

  3

  cos（2π-θ），|θ|＜

  π

  2

  ，則θ等于（　　）

  A．- π 6

  B．- π 3

  C． π 6

  D． π 3
  組卷：145引用：11難度：0.9

  解析

• 7．已知函數f（x）=2^x-

  2

  x

  -a的一個零點在區間（1，2）內，則實數a的取值范圍是（　　）

  A．（1，3）

  B．（1，2）

  C．（0，3）

  D．（0，2）
  組卷：1292引用：70難度：0.7

  解析

四、解答題：本大題共6小題，共70分，解答應寫出文字說明，證明過程或演算步驟.

• 21．已知數列{a_n}的前n項和為S_n=

  n

  2

  +

  n

  2

  （n∈N*）．
  （1）求數列{a_n}的通項公式；
  （2）設b_n=

  2

  a

  n

  +（-1）ⁿa_n，求數列{b_n}的前2n項和．
  組卷：900引用：27難度：0.3

  解析

• 22．已知函數f（x）=lnx-x.
  （1）求函數f（x）在點（1，f（1））處的切線方程；
  （2）若函數

  h

  （

  x

  ）

  =

  λf

  （

  x

  ）

  +

  1

  2

  x

  2

  只有一個極值點，求實數λ的取值范圍；
  （3）若函數

  h

  （

  x

  ）

  =

  λf

  （

  x

  ）

  +

  1

  2

  x

  2

  （其中λ＞4）有兩個極值點，分別為x₁，x₂，且

  k

  ＞

  h

  （

  x

  1

  ）

  +

  h

  （

  x

  2

  ）

  x

  1

  +

  x

  2

  在區間（0，+∞）上恒成立，證明：不等式k≥ln4-3成立．
  組卷：83引用：3難度：0.2

  解析